《赤裸裸的统计学》笔记

书名原文:Naked Statistics
ISBN 978-7-5086-4215-4
第2章 描述统计学
基尼系数、传球效绩指数都是将一系列复杂数据浓缩成一个单一数字,只是用作比较的工具,其数字本身并无实质意义。
数据只不过是知识的原材料。
描述统计学存在的意义就是简化,因此不可避免地会丢失一些内容和细节。
用回归分析的方法来完成两个关键步骤:(1)量化吃麸皮饼和患结肠癌之间的关系(例如,在其他影响癌症发病率的因素完全相同的情况下,吃麸皮饼的人患结肠癌的发病率要比不吃麸皮饼的人低 9%),(2)量化吃麸皮饼和结肠癌发病率下降之间的关系只是巧合的概率
回归分析的局限:我们可以通过统计分析来确定两个变量之间的强烈联系,但却无法解释为什么存在联系,在某些情况下,也无法确定这种联系是否为因果关系,也就是说,不知道其中一个变量的变化是否真的能引起另一个变量的变化。
中位数正好将一组数字一分为二,1/2 位于中位数之前,另外 1/2 位于中位数之后 (如果遇上一组数字的数量为偶数,那么中位数就是中间两个数的平均值)。
如果一组数据分布中没有特别离谱的异常值,那么它们的中位数和平均数差不多。
中位数将一组数据从中间分为两部分,这组数据其实还可以继续分为 4 部分,称之为“四分位数”。第一四分位数由处于底部的 25% 的数据构成,往后的 25% 的数据构成了第二四分位数,以此类推。同样的,收入分配数据还可以分为“十分位数”,每组包含 10% 的数据。如果你的收入属于美国人均收入分配顶层的那 10%,那么这意味着你要比 90% 的美国人挣得都多。我们还可以细分下去,将收入数据分为 100 份,也就是“百分位数”,每个百分位数都代表 1% 的数据,也就是说,第一百分位数表示位于底部的 1% 的人的收入,第 99 百分位数代表收入分配数据中收入最高的那 1% 的人。
这类描述性数字的好处在于,它们描述了某个具体的值在与其他数据进行比较时所处的位置。如果我告诉你,你的孩子在阅读考试中的成绩处于班级的第三百分位数(有 97% 的孩子的分数比你的孩子高),你该即刻意识到全家人应该在学习方面多辅导孩子。
标准差用来衡量数据相对于平均值的分散程度。
标准差是衡量离散的指标,反映了分散在平均值周围的数据的聚合程度。
对于许多典型的数据分布来说,有很大比例的数值都位于它们的平均数的某个标准差范围以内,这些数值有的比平均值大,有的比平均值小,但都是在一个正常范围之内。美国成年男性的平均身高为 70 英寸(1.778 米),标准差约为 3 英寸(0.0762 米),这意味着有很大一部分美国成年男性的身高在 67 英寸(约 1.7 米)到 73 英寸(约 1.85 米)之间。换言之,任何一个身高介于上述区间内的美国成年男性都不会被认为身高异常。
当然,距离平均值两个标准差的数值会减少,3~4 个标准差的数值就更少了。以身高为例,如果一个美国成年男性高于平均身高 3 个标准差,那么他的身高至少为 79 英寸(约 2 米多)。
在描述统计学中,方差很少被直接用于结论当中,往往是作为计算标准差的中间环节,而标准差才是一个更为直观的描述性数据,标准差就是方差的平方根。
最常见的分布之一:正态分布。数据的分布一般来说都是对称的,以平均数为中轴呈现类似于“钟”的形状,
美国成年男性的身高分布也是对称的,要么比 70 英寸的平均身高略高,要么略低,而且越接近平均身高,人数越多。
每一次 SAT 考试都经过精心设计,以得到一个平均分为 500 分、标准差为 100 的成绩的正态分布。
通过定义就能知道,有多少数值位于平均值一个标准差的范围之内(68.2%),有多少数值位于两个标准差的范围以内(95.4%),还有多少数值位于 3 个标准差的范围以内(99.7%),以此类推。
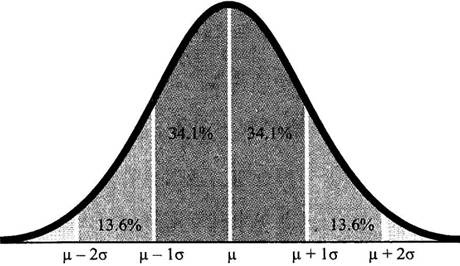
中间的那条线代表平均值,通常由希腊字母μ表示;标准差通常由希腊字母σ表示;每条色带均代表一个标准差
计算百分数差(或变化)的公式是这样的:(新数据-原数据)/原数据。分子(分数的上半部分)就是变化的绝对值,分母(分数的下半部分)的作用是将这一变化与原数据进行比较,也就是为变化添加背景。
一个“绝对”分数、号码或数字具有一些与生俱来的意义。
一个“相对”值或数字只有在比较或处于一个更大的背景中时才有意义。
描述统计学经常会比较两个数据或数量。例如,我比我的哥哥高 1 英寸,今天的气温比历史平均值高 9 摄氏度等。这些比较之所以易于理解,是因为我们大部分人都对其中所包含的数量单位并不陌生。但如果我告诉你,某品牌麦片中 A 配方的钠含量要比 B 配方高 31 毫克,除非你恰好懂得很多关于钠的知识(以及该品牌麦片的食用分量),否则上面这句话并不能给你带来特别具体的信息。又或者我对你说,我的外甥阿尔在 2013 年比 2012 年少挣了 5.3 万美元,我是不是应该对他表示担心呢?阿尔也许是一位对冲基金经理,5.3 万美元只不过是他年薪的一个零头。
在钠含量和收入这两个例子里,我们都缺少背景资料。赋予这些比较型数据意义的最简单的方法就是使用百分比。如果我跟你说,某品牌麦片 A 配方的钠含量比 B 配方高了 50%,我的外甥阿尔在 2013 年的收入与 2012 年相比减少了 47%,是不是就更容易理解了?用百分比来表示变化,可以让我们有一种用刻度测量的感觉。
伊利诺伊州的个人所得税税率由原来的 3% 上调到了 5%,有两种不一样的说法来描述这一税率的变化。主张并促成这次个税改革的民主党指出,伊利诺伊州的个人所得税税率上升了两个百分点,从 3% 上涨到 5%,共和党指出,该州的所得税税率上升了 67%。
将一系列复杂的数据序列减少为几个能够起到描述作用的数字,如奥运会体操比赛中将一套多难度组合的复杂动作浓缩为一个得分:9.8。
指数的缺点:我们有各种各样的方式来浓缩信息,每种方式都有可能导致一个不同的结果。所有指数均取决于其构成的描述性数据以及它们的权重,任何一点儿微小的变化都有可能引起结果的改变,因此,即使是最终得到的那个指数,可能是一种情况不完美但有现实意义的,也可能是完全不合理的。举一个前一种情况的例子——联合国的人类发展指数(HDI),这是一个比单纯的收入更加广泛的经济健康衡量指数。人类发展指数将收入作为评价的组成部分之一,同时还考虑到了寿命和受教育程度。美国在人均经济产出方面位居世界第 11 位(排在卡塔尔、文莱、科威特等几个石油国家之后),但在人类发展方面跃居全球第 4 名。的确,如果人类发展指数里的组成指标发生变化的话,最终的排名也会不一样,但可以肯定的是,只要是符合常理的调整,无论如何都不会出现津巴布韦超越挪威的结果。当我们想要了解全世界各地人民生活水平的差异时,人类发展指数为我们提供了一个简单方便且相对准确的排名。
要评价美国“中间阶级”的经济状况,我们需要了解(通货膨胀调整后的)工资中位数在过去几十年中的变化,他们还建议我留意一下处于第 25 百分位数和第 75 百分位数人群的工资变化,因为这两拨人通常被认为是中产阶级中的高收入和低收入人群。
还有一组必须分清楚的概念就是,在评价经济状况的过程中,不能将收入和工资等同起来。这两者是不同的,工资是我们付出的固定份额的劳动所得,如时薪或周薪;收入是全部所得的总和,来源有多种。如果一个工人找了一份兼职,或者加班很多个小时,那么这个人的收入会增多,但工资却没有发生变化。这就说明,即使一个人的工资下降,他的收入依然有可能上升,如果他加班足够多的话。但如果这些人不得不付出更多的劳动来取得更多的收入,那么我们很难评价他们的整体生活质量到底是更好还是更糟。因此,相比于收入来说,工资是评价美国人劳动收益的一个更加直观的指标,工资越高,工人们每工作 1 小时能领到的钱也就越多。说了那么多,下面我们来看一幅过去 30 年美国人工资水平的变化图,在图中
我还加入了第 90 百分位数人群的数据,以此对比相同时间内中产阶级工人和 10% 最富裕人群的工资增长水平。
(单位:美元)
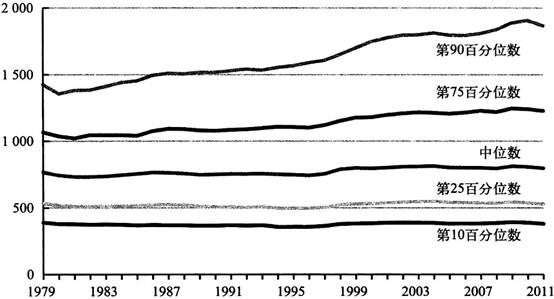
资料来源:《1979〜2009年美国工人时薪分配变化》,美国国会预算办公室,2011年2月16日。图中具体数据参见http://www.cbo.gov/sites/default/files/cbofiles/ftpdocs/120xx/doc12051/02-16-wagedispersion.pdf
从这些数据中,我们可以得出有关中产阶级经济状况的各种结论,但都不会共同指向一个唯一“正确”的答案。从中我们能看到,典型的美国工人挣着中位数工资,在原地踏步了将近 30 年;但处于第 90 百分位数的富人们就好多了。
第3章 统计数字会撒谎
9200 万美国人享受减税待遇,人均减税额超过 1000 美元 (具体数字应该是 1083 美元)。这个关于减税政策的概括准确吗?
是不是会有 9200 万美国人将享受减税待遇?答案是肯定的。
但大部分人都不能少缴纳约 1000 美元税款,因为减税额的中位数还不足 100 美元。
只有数量相对少的巨富们才有资格享受大额减税,而正是这些人拉高了平均值,让人均减税额看起来比绝大多数美国人真正享受到的要高。中位数对异常值并不敏感,因此在这个例子中,如果要看政府的减税政策对普通家庭的影响,中位数是更为准确的描述性数据。
也正是因为中位数对异常值不敏感,所以在某些情况下中位数同样会掩盖事实真相。假设你患上了某种不治之症,好消息是有一种新药刚刚研发出来,可能会对你的病产生积极疗效,坏消息是这种药的价格非常昂贵,而且副作用有很多。医生告诉你这种新药能够延长患此疾病的病人的“半数预期寿命”(也就是这些病人寿命的中位数)达两周。这根本就算不上是什么好消息,相比起那么贵的药价和不良反应,这两周的寿命不要也罢。同时,你的保险公司也拒绝为这项治疗承担费用。这是一个基于半数预期寿命的典型案例。
但在这个例子中,中位数或许会成为一个相当有误的数据。假设有许多病人对这种新药完全没反应,但同时也有相当数量(30%~40%)的病人完全治愈了。然而,后者的成功并不能在中位数中得到体现(虽然接受新药治疗的病人的平均寿命看上去非常令人振奋)。对你而言,与你自己高度相关、真正影响你决定的反而是那些接受了新药治疗并活了很多年的病人,也就是统计学里的异常值。进化生物学家史蒂芬·杰·古尔德曾经被诊断出患有某种癌症,他的半数预期寿命只有区区 8 个月。但 20 年过去了,古尔德死于另一种不相关的癌症。古尔德生前写过一篇非常有名的文章,题目为“中位数不等于真信息”,他在文章里指出了他只能活 8 个月是一个错误结论,并表示是他头脑里积累的统计学科学知识将他从错误的结论中拯救了出来。中位数的定义告诉我们有 1/2 的病人活不到 8 个月,但另外 1/2 的病人至少可以活 8 个月,或者比 8 个月 的时间更长(甚至是活到老),其死亡分布是“右偏”的。因此,如果你恰好患上了这种病,这一数据的意义要比一个单纯的技术术语丰富得多。
上述例子表明,中位数的决定性特征——不考虑数据距离中间位置有多远或是多近,而是关注它们是高于中间位置还是低于中间位置——反而成为它的弱点。与之相反,平均数恰恰是由数据分布决定的。从准确性的角度来看,平均数和中位数孰取孰舍,关键就在于这个数据分布里的异常值对事实的真相是起到扭曲的作用,还是其重要的组成部分。再次强调,判断比数学更重要。当然,没有人强制你一定得选中位数或平均数,任何一个复杂综合的数据分析都会包含这两个数据。所以,当只有其中一个数据出现的时候,你就要注意了,有可能只是出于言简意赅的考虑,但也有可能是某些人别有用心地想用数据“说服”你。
经济学家甚至为这一重要的现象冠以专业术语,以表示相关数据是否考虑了通货膨胀因素。名义数据就是没有就通货膨胀做出调整的数字,比较 1970 年某项政府项目的名义花费与 2011 年政府在相同项目上的名义花费,实际上看的仅仅是政府财政部在这两年所开出的支票的票面金额,并没有考虑 1970 年的 1 美元能买的东西比 2011 年买到的东西多。假设政府在 1970 年时为老兵的住房补助项目投入了 1000 万美元,到了 2011 年,政府在此项目上投入了 4000 万美元,联邦政府在这个项目上的努力实际上是退步了。花费的金钱在名义上的确是增多了,但这并没有反映出美元价值的变化。1970 年的 1 美元相当于 2011 年的 5.83 美元,也就是说政府 2011 年需要在老兵的住房补助项目上投入 5830 万美元才是与 1970 年的 1000 万美元持平。
实际数据是考虑了通货膨胀因素并做出调整的数字。最常见的方法就是将所有数据统一换算成一个相同的单位,如 2011 年的美元。
美国最低工资标准是由美国国会制定的。当前的最低工资标准为每小时 7.25 美元,这是一个名义值。你的上司才不会理会现在的 7.25 美元能买到的东西是不是和两年前一样多,他只需要保证能够支付给你的时薪不少于 7.25 美元。上司只跟你谈支票上的数字,而非该数字背后的购买力。
随着时间的推移,通货膨胀会逐渐削弱最低工资的购买力(以及其他名义工资的购买力,这也是为什么工会代表在与雇主谈判时总会谈到“生活成本调整”的问题)。如果商品价格的上涨速度快于美国国会调高最低工资的速度,那么每小时能够获得的最低工资的实际价值就会缩水。最低工资标准的支持者们应该关注这一工资的实际价值,因为这项法律出台的初衷就是为了保护低收入工人的利益,保证他们每小时的劳动所获得的报酬能够换来一定水平的购买力以维持生活,而不是让他们在付出劳动后却得到一张什么都买不起的大额支票。
好莱坞在比较不同年份的电影票房时,总是会对通胀因素视而不见,或许是因为无知,但更有可能是出于对利益的考虑。
截止到 2011 年,史上最卖座的 5 部电影依次为:
- 《阿凡达》(2009)。
- 《泰坦尼克号》(1997)。
- 《蝙蝠侠前传II:暗黑骑士》(2008)。
- 《星球大战IV》(1977)。
- 《怪物史莱克II》(2004)。
这个排名看上去是不是有点奇怪?好莱坞最常做的事就是让最新的大片看上去比上一部的场面更大、更加成功。为达到这个目的,好莱坞(以及负责媒体电影报道版块的记者)很少用名义数据,因为这一做法会让现在的电影在票房上很轻易地超过 10 年、20 年或者是 50 年前的电影——谁都知道现在的票价比以前贵多了(当《乱世佳人》在 1939 年上映的时候,那时美国某地的一张电影票售价只有 0.5 美元)。比较不同时期电影的商业成功最准确的方法就是,考虑了通货膨胀因素后做出调整的票房成绩。1939 年 1 亿美元的票房可比 2011 年 5 亿美元的票房壮观多了。这样来看,将通货膨胀考虑在内,美国史上最卖座的 5 部电影是:
- 《乱世佳人》(1939)。
- 《星球大战IV》(1977)。
- 《音乐之声》(1965)。
- 《外星人E·T》(1982)。
- 《十诫》(1956)。
以剔除通胀因素的实际票房成绩来看,《阿凡达》只排到了第14位,《怪物史莱克II》则落到了第31位。
研究人员有时候会特别指出某项增长数据是由“一个较低的基数”得出的,哪怕是很小的一点儿增长在进行百分率比较时,看上去都会很可观。
除此之外,百分率的另一面也是很可怕的,那就是一个庞大数额的微小比例也会是一个很大的数字。如果美国国防部部长说,2013 年的军费开支仅增长 4%——这看上去可是一条好消息啊!作为纳税人的我们,是不是应该庆祝?其实并不尽然,因为美国的国防预算是在 7000 亿美元左右,4% 的比例就是 280 亿美元,这笔钱能买多少个火鸡三文治啊!事实上,区区 4% 的军费开支就已经超过了美国国家航空航天局(NASA)的全部预算,相当于美国劳工部和财政部预算的总和。
同样的,想象一下你有一个菩萨心肠的老板,出于公平的考虑,他决定 2013 年为公司的每一位员工加薪 10%——多么慷慨的决定啊!只不过有一点,老板的年薪是 100 万美元,而你每年只挣 5 万美元,老板将会得到 10 万美元的加薪,而你只有 0.5 万美元的加薪。“2013 年每个人都将获得 10% 的加薪”听上去要比“我的加薪是你的 20 倍”好受太多了——虽然这两句话都没错。
考核学校和教师最常用的方法就是看学生的考试分数,统考结束后,学生的优异成绩就是教师和学校最好的金字招牌;与之相反的,糟糕的成绩无疑会释放出一个清晰的信号:相关教师应该被辞退,而且越早辞退越好。这样看来,仅凭考试分数我们就能彻底改善公共教育系统了,对吗?
错。
学生的学业表现有好有差,但其中有多少比例要归功或归咎于学校(或所在的班级)呢?
从小就生活在衣食无忧、书香门第家庭里的孩子,一般来说从进入幼儿园的第一天起就有可能会比别的孩子的成绩好。相反的情况同样成立,有些学校的学生天资平平,虽然教师教得很好,但是学生的成绩还是处在一个低水平上,如果没有这些老师的付出,那些学生的成绩会更加惨不忍睹。所以,我们需要在学校,甚至班级层面上将一些“附加值”纳入考核。学生成绩的绝对水平对于解答我们的问题没有意义,我们想知道的是这些学生的表现中有多少是受到了学校和教师的影响,我们想要评估的其实是这些教学因素。
有人会说这并不难,只需要在开学时给学生安排一场摸底考试即可,再将这次考试的成绩与入学之后的考试成绩进行对比,就能够判断学生的学业是进步了还是退步了,并由此对其所在的学校或班级进行评价。
但这种方法还是错误的。不同能力或背景的学生在学习上的进步程度也是不同的。一些学生在领会知识点方面就是比其他学生快,而这与老师的教学质量没有关系。假如让优质学校 A 的学生和各方面都稍差的学校 B 的学生同时开始学习相同难度的代数课,一年以后,A 校学生的代数成绩更理想,原因可能是 A 校的教师教学能力更强,也可能是 A 校学生的学习能力更强,还有可能二者兼有。
我们所有关于寻找“最佳”学校的努力都有可能适得其反,误导大众。
每年秋天,芝加哥的几家当地报纸和杂志都会对该区域内的高中进行一次排名,其主要参考依据通常是州考成绩。从统计学的角度看,这些排名难免会有一些让人捧腹的地方,比如常年位居榜单前几位的都是一些选择性招生的学校,意思是说学生要进入这些高中,就必须提出申请,申请者中只有很小一部分的人能够如愿,而这些学校在挑选学生时最重要的参考依据就是学生的统考成绩。我们就这个问题作个小结:(1)这些学校因其学生在州考中的出色发挥而被认为是“优质”学校;(2)要进入这些学校学习,首先学生要有非常高的考试分数。
在考试分数的统计过程中,也出现了同样恶劣的作弊现象。提高考试成绩的方式之一就是改善教学质量,这样学生就能学到更多的知识,并且在考试中取得进步,改善教学质量确实是较好的方法。而比较差的方法则是想办法让那些成绩最差的学生“远离”考场,即使剩余参加考试的学生的成绩没有任何长进,最终考试的平均成绩也会有所提升。
纽约州就因为类似的统计陷阱而栽了大跟头,付出了惨痛的代价。州政府之前出台了“记分卡”制度,对接受心脏搭桥手术的病人的死亡率进行统计,以便让公众在选择心脏科医生时有一个参考。这似乎是一个完全合情合理,而且有所帮助的描述统计学在政策制定过程中的应用。心脏搭桥手术是治疗心脏病最常用和有效的方法,心脏病人在搭桥手术过程中的死亡比例当然是一个非常重要的数据,而作为个人根本没有办法了解到确切数据,因此政府出面收集并向公众公开这一数据是合乎情理的。但就是这么一个“好”政策,却导致了更多病人的死亡。
心脏科医生肯定会在意他们的“记分卡”。但是对于一个外科医生来说,降低病人死亡率最简单的方法并不是降低病患死亡人数,因为大部分医生在救死扶伤方面已经竭尽全力了。降低死亡率最简单易行的方法是拒绝为那些病况最严重的病人动手术。罗彻斯特大学医学与牙医学院的一项调查表明,以服务病人为初衷的记分卡,到头来反而会给病人造成伤害:在参与调查的心脏科医生中,有 83% 的医生表示正是由于公开了死亡率数据,一些本来可以从搭桥手术中获益的病人最终没能被安排进行手术;79% 的医生表示收集并公开死亡率数据或多或少地影响了他们的治疗决策。这一看似有用的描述性数据存在一个可悲的矛盾,而心脏科医生也只能理性地接受并釆取自己的对策,就是让那些最需要心脏搭桥的病人远离手术台。
第4章 相关性与相关系数
相关性体现的是两个现象之间相互关联的程度。
如果一个变量的改变引发另一个变量朝着相反的方向变化,那么这两个变量就存在负相关性。
有些时候也会出现与相关性相违背的现象。有些个子矮的人就是比个子高的人重一些,有些从来不运动的人甚至比运动爱好者苗条,但无论怎样,身高与体重、锻炼与体重之间总是存在着有意义的关联。
相关性作为一个统计工具的魅力就在于将两个变量的关联精炼成一个描述性数据:相关系数。
相关系数是一个区间为 -1 到 1 的常数。如果相关系数为 1,即完全相关,表示一个变量的任何改变都会导致另一个变量朝着相同方向发生等量的改变。如果相关系数为 -1,即完全负相关,代表一个变量的任何变化都将会引发另一个变量朝着相反方向发生等量的改变。
相关系数越接近 1 或 -1, 变量间的关联性就越强。如果相关系数为零(或者接近零),则意味着变量之间不存在有意义的联系。
相关系数不受变量单位的限制。我们可以计算身高和体重之间的关联性,哪怕身高和体重的单位分别是英寸和磅。我们甚至还可以计算出高中生家里的电视机数量和他们的考试成绩之间的关联性,而且我敢保证是正相关。这就是相关系数能够为我们完成的一件非常神奇的事情:将大量芜杂无序、单位不统一的复杂数据(就比如上面的身高、体重散点分布)加工成一个简洁、优雅的描述性数据。
相关系数的计算过程如下:
- 计算出两个变量的平均数和标准差。还是以身高和体重为例,我们会得出样本人群的平均身高和平均体重,以及它们的标准差。
- 对所有数据进行转换,表现为距离(也就是标准差)的形式。
假设样本的平均身高为 66 英寸(标准差为 5 英寸),平均体重为 177 磅(标准差为 10 磅)。如果你的身高为 72 英寸,体重为 168 磅,就表明你高于平均身高 1.2 个标准差,用公式来表述即为 [(72-66)/5]=1.2, 轻于平均体重 0.9 个标准差 , 即 [(168-177)/10]=-0.9。的确,如果你的身高高于平均身高,体重却轻于平均体重,我们可以用“异常”来形容。注意了,在此之前你的身高和体重数据后面还紧跟着单位——“英寸”和“磅”,现在却被转换成了简简单单的 1.2 和-0.9,单位神奇地消失了。
- 到了这一步,只需要让电脑完成剩下的工作。通过公式,电脑会整合样本里所有人的身高和体重的标准差数据,并最终为我们揭示身高和体重之间的关系。假如样本中有些人的身高高于平均值 1.5 或 2 个标准差,那么他们的体重相对于平均值来说会呈现一种什么状况?那些身高接近平均值的人,他们的体重又会有什么变化?
如果一个变量和平均值之间的距离与另一个变量和平均值之间的距离在相同方向上高度吻合(例如,身高特别高或矮的人的体重一般也会特别重或轻),那么我们就可以断言这两个变量之间存在着强烈的正相关关系。
如果一个变量和平均值之间的距离与另一个变量和平均值之间的距离在相反方向上高度吻合(例如,锻炼时长大大高于平均值的人,他们的体重也大大低于平均值),那么我们就可以断言这两个变量之间存在着强烈的负相关关系。
如果两个变量无论在什么分析模式下都无法呈现出规律(例如鞋的尺码和锻炼时长),那么这两个变量之间就不存在或基本不存在相关性。
SAT 测试的初衷就在于“让每位学生在申请大学时都能得到公平的对待”。SAT 将学生能力标准化加工,让大学在录取学生时有了简单明了的参考标准。但 SAT 测试究竟是不是一个好的能力评价标准呢?想要找一个评价学生的统一标准并不难,我们可以让所有的高中毕业生来一个百米测试,也能分出优劣,而且比 SAT 花费少和易于操作。不过有一个问题,百米短跑的成绩与大学表现可以说毫不相关,这是两个不相关的变量,虽说数据收集并不费劲,但它也不会告诉我们有意义的情况。
那么,SAT 在这方面的表现如何?我有一个不幸的消息要告诉未来的高中毕业生,SAT 成绩在预测大学一年级学生的成绩方面表现得相当不错。美国大学委员会定期会发布相关性报告。零代表毫不相关,1 代表完全相关,学生的高中平均成绩与大学第一年的平均成绩之间的相关系数为 0.56(为了让大家有一个直观的比较,我为大家提一个数据,那就是美国成年男子身高和体重之间的相关系数大约为 0.4), 而 SAT 综合成绩(阅读、数学和写作)与大学第一年的平均成绩之间的相关系数同样为 0.56。既然 SAT 测试在预测学生大学表现方面并没有比高中的平均成绩更优秀,那为什么还要设立这样一个考试呢?事实上,如果将 SAT 成绩和高中平均成绩综合起来,就能得到一个相关系数为 0.64 的最佳预测指数。所以,亲爱的同学,我只能说抱歉了,乖乖地准备 SAT 考试吧。
我们必须牢记一点,那就是相关关系并不等于因果关系。两个变量存在正相关或负相关的关系,这并不代表其中一个变量的改变是由另一个变量的变化引起的。
第5章 概率与期望值
1981 年,美国约瑟夫·施利茨酿酒公司斥 170 万美元巨资为该公司旗下的旗舰品牌——施利茨啤酒开展了一场大胆而冒险的市场营销活动。当美国橄榄球超级杯大赛(即“超级碗”)的中场休息时间一到,施利茨公司就会当着全球亿万电视观众的面,现场直播一场别开生面的啤酒品鉴会,而挑选的对手不是别人,正是施利茨的死对头——米切罗啤酒,更让人大跌眼镜的是,参加品鉴会的不是别人,正是 100 名米切罗啤酒的忠实用户。这样的广告从始至终出现在季后赛的每一场比赛当中。类似的电视直播啤酒品鉴会总共有 5 场,每场都会邀请 100 名某品牌啤酒的“拥趸”,包括百威、米勒、米切罗等,让这些啤酒爱好者在自己最钟爱的啤酒和施利茨啤酒之间进行“盲品”。一边是如火如荼正在进行的职业橄榄球季后赛,一边是同样激烈的啤酒品鉴会,那时的广告标语甚至打出了“看季后赛,喝施利茨啤酒”的字样。
广告噱头很明确:即使是那些自认为喜欢另一种品牌的啤酒爱好者,在盲品时也会发现自己更偏爱施利茨啤酒。啤酒公司甚至还请了一位橄榄球职业联赛的前裁判来监督整个活动过程。考虑到在数量众多的电视观众面前举办这样一场充满风险的啤酒品鉴会,你肯定会觉得施利茨啤酒的口感一定特别好,否则哪会有勇气搞这样的宣传,是吗?
那可不一定。施利茨只需要生产出口感平平的啤酒,再掌握一些扎实的统计学知识,就能确保这项计谋肯定会成功——注意,我在写作时通常会非常谨慎地使用“计谋”这样的词,尤其是列举啤酒广告这样的例子。施利茨所生产的这种啤酒喝起来没什么特别的,跟绝大多数其他品牌的同类啤酒几乎没有太大差别;但讽刺的是,正是这一点成为施利茨啤酒广告营销的核心。可以假定的是,如果在街上随机找几个喜欢喝啤酒的人,他们基本上区分不出施利茨、百威、米切罗或米勒啤酒。因此,取其中任意两种品牌的啤酒进行盲品测试,猜对品牌的概率基本上和扔硬币差不多。大体来看,有 1/2 的人会选择施利茨,剩下 1/2 的人会选择“挑战”品牌的啤酒,单看这样的结果可能无法构成一个有说服力的广告营销(我们总不能说“既然口感都差不多,就选择施利茨吧”)。而且,施利茨啤酒公司绝对不会拿自己的忠实用户做试验,因为差不多有 1/2 的用户会“不小心”挑选其他品牌的啤酒。如果一群原本忠实于某品牌啤酒的消费者在盲品时竟然觉得竞争对手的啤酒好喝,这个品牌该有多悲哀啊,所以,施利茨就让这样的事情发生在其他品牌身上。
施利茨的高明之处在于,只邀请那些声称自己偏爱另外一个品牌啤酒的消费者参加测试。如果盲品的结果果真如抛硬币一样,那么就会有 1/2 的百威、米勒或米切罗啤酒的爱好者最终选择施利茨。这下施利茨扬眉吐气了,因为有 1/2 的百威啤酒爱好者更喜欢喝施利茨!
更妙的是,这一切都在橄榄球联盟决赛的中场进行直播,而且由一位身穿裁判服的橄榄球前裁判执法整个盲品过程。毕竟是电视直播,就算施利茨已经私底下进行了大量试验,并证明了有 1/2 的米切罗啤酒爱好者会选择施利茨啤酒,又有谁能够保证在最终直播的时候不出岔子?万一“超级碗”直播时选取的 100 名米切罗爱好者的味觉特别灵敏呢?虽然盲品测试在概率上等同于抛硬币,但万一就是有绝大部分人恰巧选择了米切罗呢?如果我们让 100 个人排成一队,逐个抛硬币,出现 85 或 90 个硬币反面向上的可能性也是完全存在的。对于施利茨公司来说,在直播时碰上这样的情况将会对它们的品牌造成毁灭性的打击(更不必说用于购买广告时段的那 170 万美元了)。
二项分布的主要特点有,试验次数是固定的(例如 100 位啤酒盲品者),每一次试验都有两个可能的结果(施利茨或米切罗),而且每一次“成功”的概率都是相等的(假设选择任意一个品牌啤酒的概率为 50%,如果选择施利茨的概率高就表示试验“成功”)。我们同时还假定所有的试验都是各自独立的,即一位盲品者的决定不会影响其他人的选择。
有了这些信息,这位统计学的“超级英雄”就能计算出所有可能出现的不同结果的概率,如 52 人选择施利茨,另外 48 人选择米切罗,或者是 31 人选择施利茨,另外 69 人选择米切罗,这种情况发生的概率是多少。所有 100 位盲品者都选择米切罗的概率是 1/1267650600228229401496703205376, 这可能比这些人在中场休息时被陨石砸中的概率还低。重要的是,重复这些基本运算,能够让我们知道某个结果范围内的累积概率,如有不多于 40 位盲品者选择施利茨的概率是多少。这些数据足以让施利茨的市场营销人员松一口气。
让我们假设,要让施利茨公司满意,100 位盲品者中至少要有 40 位选择施利茨啤酒。这是一个非常可观的数字,因为所有参加盲品直播的人都曾信誓旦旦地声明自己是米切罗的忠实用户。而要达到这样的效果,其实一点儿都不难。如果盲品会果真如抛硬币一样,那么运用概率学的基本知识,就能得出至少有 40 人选择施利茨的概率为 98%,至少有 45 人选择施利茨的概率为 86%。从理论上来看,这场电视营销活动其实并没有很大的风险。
那么,现实中的结果又如何呢?在 1981 年“超级碗”中场休息的现场,正好有 50% 的米切罗啤酒的消费者在盲品测试中选择施利茨,不多不少,正好 1/2。
从这个例子中,我们可以得到两个重要的启示:第一,概率是一个非常强大的统计学工具;第二,20 世纪 80 年代的许多畅销品牌的啤酒确实在口感上没有什么区别。
许多事件的概率是明确的,如抛一枚标准硬币结果是正面的概率为 1/2,掷一粒骰子得到 1 点的概率为 1/6,还有一些事件的概率能够从过去的数据中推导出来。在美国职业橄榄球比赛中,触地得分后踢定位球再得一分的平均概率为 0.94,也就是说,每 100 个定位球中有 94 个会成功。当然,这一数据会随着不同球员、不同天气环境以及其他因素的改变而有所不同,但不会发生剧烈变化。在获得并信任此类信息的前提下,决策者常常能够看清风险、作出决定。举个例子,澳大利亚运输安全局发布了一份有关乘坐不同交通工具致死风险的量化报告,大家都觉得飞行非常可怕,但实际上商业航空旅行的风险是微乎其微的。澳大利亚自 20 世纪 60 年代起就再没有发生过一起商业航空致死事故,因此航空旅行每一亿公里的致死率基本为 0。汽车每一亿公里旅行的致死率为 0.5,真正吓人的是摩托车的致死率,如果你立志成为一名器官捐献者,那么你就选择摩托车出行吧,因为摩托车的致死率比汽车整整高出 35 倍。
在“9.11”恐怖袭击事件发生之后,越来越多的美国人选择自驾出行,而不选择乘坐飞机。据统计,在考虑平均死亡率和天气等导致路面交通事故因素的前提下,2001 年 10~12 月,平均每个月因交通事故致死的人数比以往多了 344 人。该效应随着时间的推移逐渐减弱,这是因为大家对恐怖主义的恐惧在慢慢消退,但这项研究的作者认为,“9·11”恐怖袭击事件导致的驾车死亡人数或已超过 2000 人。
A 与事件 B 同时发生的概率是这两个事件发生概率的乘积。举个例子可能会更直观一些,抛一枚标准硬币得到正面朝上的概率为 1/2,连续抛两次都得到正面朝上的概率为 1/2X1/2=1/4,连续抛 3 次都得到正面朝上的概率为 1/8,连续抛 4 次都得到正面朝上的概率为 1/16,以此类推。同样,连续抛 4 次硬币都得到反面朝上的概率也应该为 1/16。这也解释了为什么学校或办公室的电脑总会弹出一个对话框,提醒你提高开机密码的“安全级别”。假设你的开机密码为 6 位,而且用的全是数字,那么总共有 10x10x10x10x10x10=10^6 种数字排列组合,不要以为这种组合很复杂,对于计算机来说,不到一秒钟,就可以将这些数字排列组合全都试一遍。
有一点必须再次强调:这一公式只适用于相互独立的事件,也就是说,一个事件的发生及其结果对另一个事件不会造成任何影响。例如,你第一次抛硬币得到正面朝上的概率扦不会影响你第二次抛硬币得到正面朝上的概率。相反的,今天下雨的概率与昨天是否下雨并不是相互孤立的,因为下雨作为一种天气现象具有连续性,有时候经常连续几天都下雨。同样的,你今年出车祸的概率与明年出车祸的概率也不是相互孤立的,今年导致你出车祸的原因很有可能也会导致你明年发生类似的车祸,比如你有可能经常酒后驾车、喜欢跟别人飙车、习惯开车时发短信,或者车技很差。这也是为什么你的车险费率会在发生车祸后上升,并不仅仅是因为保险公司想要从你这里挽回一点儿它们为你支付的赔偿金,更重要的是,它们拥有了关于你未来发生车祸概率的新信息——当你开车撞向你的车库大门之后,这个概率就上升了。
假如你对发生这个事件或发生那个事件的概率感兴趣,也就是出现结果 A 或出现结果 B 的概率(再次假设两个事件是相互独立的),这个概率就是 A 和 B 各自的概率之和:A 概率+B 概率。举个例子,掷一次骰子得到 1 点、2 点或 3 点的概率就是它们各自的概率之和:1/6+1/6+1/6=3/6=1/2。
通过概率的计算,我们还可以得到在所有管理决策的过程中,尤其是在金融领域是最实用的统计工具:期望值。期望值是基础概率学的升级版。某个事件如买彩票的期望值或收益,实际上就是所有不同结果的和,其中每个结果都是由各自的概率和收益相乘而来。跟往常一样,我们还是用例子来说明这个问题。假设你参与了一个掷骰子的游戏,游戏规则是掷出 1 点可以获得 1 美元,掷出 2 点可以获得 2 美元,掷出 3 点可以获得 3 美元,以此类推。那么在这个游戏中,掷一次骰子的期望值是多少?每一个结果都有 1/6 的概率,因此期望值为:
1/6(1 美元)+1/6(2 美元)+1/6(3 美元)+1/6(4 美元)+1/6(5 美元)+1/6(6 美元)=21/6, 即 3.5 美元。
粗略看一下,3.5 美元的期望值似乎是一个无效数据,毕竟你不可能掷一次骰子就获得 3.5 美元。但事实上,期望值是一个非常有用的参考数据,通过比较成本投入和期望收益,你就能知道做这件事是不是“值得”。如果在上述游戏中,每掷一次骰子需要缴纳 3 美元,你还玩吗?当然,因为期望回报(3.5 美元)要高于游戏成本(3 美元)。这虽然并不代表你第一次玩就保证能赚到钱,但至少可以帮助你认清哪些事情值得冒险。
我们可以进一步将期望值延伸到美国职业橄榄球领域。之前提到,在比赛中触地得分之后,球队将会面临两个选择,要么直接射门再得一分,要么进行一次两分投球的尝试。如果选择前者,则在三码线处定点踢球穿过球门柱即可;如果选择后者,则需要从三码线处将球带到或传到球门区把对方逼成死球,可以想象其难度之大。因此,球队可以选择简单的打法得 1 分,也可以选择难度高的打法得 2 分。应该怎么选?
在前文中已经提到,触地后成功点射的概率为 0.94,也就是说这一尝试的期望值为 0.94, 因为回报(1 分)乘以成功概率(0.94)得到的结果为 0.94 分。没有队伍能在比赛中打出 0.94 分,但这个数字能够量化触地后的一种选择,从而与另一种选择——2 分尝试进行直观的比较。2 分尝试的期望值要低得多,才 0.74 分,虽然回报很高(2 分),但成功率却低得可怜(0.37)。由此可见,如果比赛只剩下一秒钟的时间,一支队伍在触地得分后还落后对手 2 分,这支队伍别无选择,只能进行 2 分尝试;但如果某支队伍处于领先,其目标只是在比赛中扩大比分优势,那么就应该采取得 1 分策略。
我们还可以解释为什么永远不要买彩票。在伊利诺伊州,每张彩票的背面都印着不同玩法和等级的中奖概率,假如我买了一张 1 美元的即开型彩票,在彩票背面印着的细小文字里我可以找到不同等级奖金的中奖概率:1/10(1 美元,即免费再来一张)、1/15(2 美元)、1/42.86(4 美元)、1/75(5 美元),一直到概率为 1/40000 的 1000 美元。我将每一个等级的中奖概率乘以奖金额度,最后将得到的结果相加,计算出购买此类彩票的期望值。结果是这种 1 美元彩票的回报期望值约为 0.56 美元,所以这绝对是一项糟糕的投资。但我的运气还不错,中了 2 美元。
虽然我中了 2 美元,依然无法改变购买彩票是一种愚蠢行为的事实,这就是概率教给我们的重要经验之一。通过概率计算得出的好决策,有时会得到坏的结果;而坏的决策——如在伊利诺伊州购买 1 美元即开型彩票——有时还是会有好处,至少从短期来看是这样。但最终“笑傲江湖”的还是概率,因为谁也打败不了概率。有一个重要的定律叫作大数定律,即随着试验次数的增多,结果的平均值会越来越接近期望值。是的,我今天买彩票的确中了 2 美元,我明天也有可能再中 2 美元,但如果长年累月地买下去,每天买的都是这种预期回报为 0.56 美元的 1 美元即开型彩票,那么赔钱将是毋庸置疑的事,到了买齐 100 万张彩票的那一天(也就意味着我花了 100 万美元),我最终的中奖金额约为 56 万美元。
我们也可以用大数定律来解释为什么赌场从长期来看总是挣钱的问题。赌场内所有项目的概率都是有利于赌场老板的(出“老千”的赌客不考虑在内)。如果赌场的营业时间足够长,吸引的下注人数也足够多,那么赌场从赌桌赚到的钱肯定要比付出的要多。通过大数定律,我们还可以解释为什么施利茨要在“超级碗”中场休息时邀请 100 位而不是 10 位啤酒爱好者来参与啤酒盲品测试。下面是“施利茨型”测试的“概率密度函数”,测试人数分别为 10、100 和 1000。不要被这个函数的名称吓到,其实函数本身并不复杂,X 轴罗列了各种可能出现的结果,Y 轴表示的是对应结果出现的概率。需要在这里重申一遍的是:我们的前提是所有品牌啤酒的口感是差不多的,品尝选择的过程类似于扔硬币,每位盲品者选择施利茨的概率都为 50%。我们可以从以下的 3 幅函数图中看到,随着盲品者人数的增多,越来越多的预期结果向中间(也就是有一半的人选择施利茨啤酒)集中;与此同时,位于曲线两端的极端结果出现的概率则下降得非常厉害。
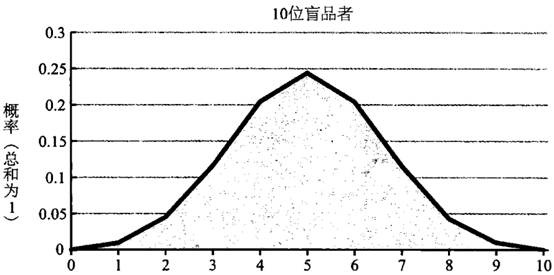
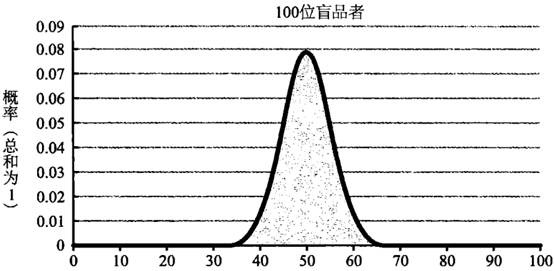
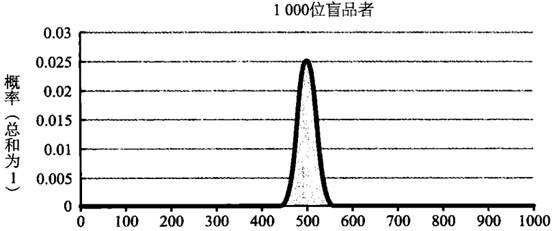
在前文中我说过,如果有大于或等于 40% 的米切罗啤酒爱好者在盲品测试中选择了施利茨啤酒,那么施利茨的高层就满意了。下面就列举了不同盲品人数的条件下得到满意结果的概率:
10 人:0.83。
100 人:0.98。
1000 人 :0.9999999999。
1000000 人:1。
读到这里,我想很多人已经能够领会“千万别为标价 99 美元的打印机购买保修延长服务”的含义了。整个保险行业都是建立在概率的基础之上,保修只不过是保险的一种表现形式而已。
预期损失和预期值是完全相同的概念,只不过是套上了保险的外衣。假设车的赔偿额度为 4 万美元,每年被盗的概率是 1/1000, 那么该车的年预期损失为 40 美元,车险保费组成中盗窃险种的定价就应该高于 40 美元,这样看来,保险公司和赌场、伊利诺伊州彩票的性质是一样的,它们都需要付出,但从长期来看,得到的肯定要比付出的多。
作为消费者,你应该知道,从长远来看,保险并不能为你省钱。保险能为你做的是,当你遭遇一些难以承受的巨大损失时,如价值 4 万美元的汽车被盗、35 万美元的房子被烧毁等,为你提供赔付,帮你渡过难关。从统计学的角度来看,购买保险是一项“糟糕的投资”,因为平均来看,你支付给保险公司的钱永远要比得到的赔付多。但如果想防止一些足以毁掉你生活的结果出现,保险就是一个理性的工具。讽刺的是,一些巨富如巴菲特倒是可以不用买车险、房屋险,甚至医疗保险,从而省下不少钱,因为就算有再糟糕的事情发生在他的身上,他都能承担得起。
假设你刚刚精挑细选了一台好评如潮的激光打印机。当你结账的时候,销售人员会向你提供一份详细的保修延长清单,比如说额外支付 25 美元,可以延长一年的免费修理或更换服务,支付 50 美元可以延长维修服务两年。现在你对概率、保险以及基础经济学已经有了一些基本的了解,你可以很快联想到以下几点:(1)百思买是一个以赢利为目的的商家,因此追求利润最大化是它不变的追求;(2)销售助理正在竭尽所能地劝你购买保修延长服务;(3)从前两点能够推测出,购买保修延长服务的代价要高于商家为你修理或更换打印机的预期成本,如果不是这样,那么商家就不可能会如此卖力地推销了;(4)就算价值 99 美元的打印机坏了,你需要自掏腰包来修理或换一台新机器,也不会给你的生活造成太大的困扰。
一般来说,你为延长保修服务所支付的金额要高于打印机的修理费。你应该时刻谨记为那些你无法轻松承受的意外上保险,而其他情况就不要浪费钱了,这是个人理财的核心原则之一。
有些事情可能会在不同时间段出现意外状况,在面临这类复杂抉择时,预期值同样能够帮助我们理清思路。假设你的一个朋友建议你向一家研究中心投资 100 万美元用于开发男性防脱发产品,你或许会问成功的概率有多大,而你的朋友的回答很复杂。由于这是一个研发项目,因此研发团队研制成功的概率只有 30%, 如果最终研制产品失败了,那么你将收回 25 万美元,因为这部分资金原本是留着用于市场推广(用户测试、广告宣传等)的;即使最终产品研制成功了,美国食品药品监督管理局认为这一神奇的治疗脱发的产品对人体安全并批准进入市场的概率也只有 60%; 到了那个时候,即使我们的产品安全有效,依然还有 10% 的概率会出现一个强劲的竞争对手,带着更好的产品与我们一同进入市场,占据全部的市场份额。如果一切顺利——产品安全、有效,而且竞争者也没有出现,那么你将获得最多 2500 万美元的投资回报。
你动心了吗?
朋友提供的信息量令人眼花缭乱。潜在的回报很诱人,回报的金额是投资额的整整 25 倍,在这一过程中,同样充满了各种潜在的陷阱和失败。如果每一个结果的出现概率都是准确的,那么画一张决策树形图,能够帮助我们理清信息,决定下一步应该做什么、怎么做。决策树形图标出了每一个不确定因素的来源,还有所有可能出现的结果及其概率。在树形图的下方,给出了所有回报可能的金额和概率。如果我们将每一个回报额乘以概率,再将得到的结果相加,就可以算出这一投资机会的期望值。通过观看下图能够帮助我们更好地理解问题。
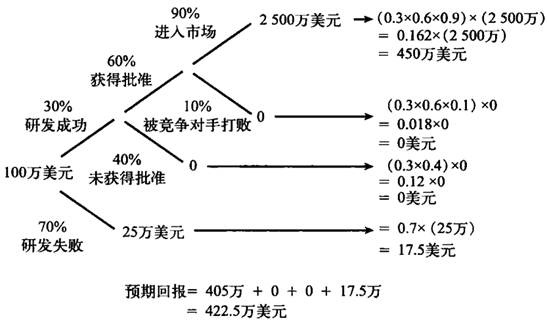
如此看来,这项投资的预期回报是非常诱人的,高达 422.5 万美元。但我还是不建议你用辛辛苦苦积攒的、准备将来给孩子读大学的钱来进行投资。观察决策树形图,你会发现预期回报大大高于一开始的投资额,但不要忘记,最有可能发生的结果是研发失败,以致治疗男性脱发的产品最终没有面世,而你只能拿回剩下的 25 万美元。至于你对这项投资的胃口到底有多大,就要取决于你的风险倾向了。对此,大数定律给出的建议是,对于一家投资公司或像巴菲特这样富可敌国的个人投资者来说,应该尽可能地发掘上述例子这类结果不确定但预期回报很丰厚的投资机会,而且数量越多越好,几百个项目里面肯定有一些会成功,一些会失败,但平均来看,这些投资者最终会像保险公司或赌场那样挣到大钱。如果预期收益对你有利,那么涉足的项目越多,赚钱的机会就越大。
同样的道理,我们还可以用来解释一个有违直觉的现象。有时候,针对全美国人口监测如艾滋病这类罕见但严重的疾病是行不通的。假设我们对某种罕见病的检测拥有相当高的准确度,举例来说,每 10 万人中会有一个人患上某种疾病,检测准确率为 99.9999%,可以保证在检测过程中不产生一例伪阴性(也就是从不漏过任何一个患上该病的人),但产生伪阳性(也就是一个没有患上该病的健康人被误测为阳性)的概率为万分之一。这样就会导致一个棘手的状况,虽然这种疾病的检测准确率非常之高,但绝大部分被诊断为阳性(也就是患有该疾病)的人实际上根本没有得此病。这会在那些诊断结果为阳性的人群中产生巨大恐慌,后续的检测和治疗也会浪费有限的医疗资源。
如果我们对美国所有成年人,即约 1.75 亿人口进行检测,决策树形图如图 5-5 所示。
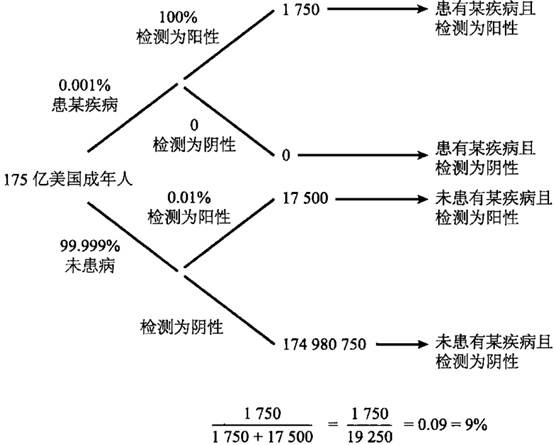
只有 1750 位成年人患有该疾病,他们的检测结果均为阳性。有超过 1.74 亿 成年人未患病,在这部分健康人群中,有 99.999% 的人得到了正确的检测结果,只有 0.01% 的人被误检为阳性。但 1.74 亿的 0.01% 依然是一个非常大的数字,因此在实际操作中平均将会有 1.75 万健康的人被告知患有该疾病。
这意味着什么?我们一起来分析一下。总共有 19250 人的检测结果为阳性,但真正患病的只有 9%,而且这还是一个准确性非常高、伪阳性非常低的检测。我想不需要作太多解释,大家就能理解为什么在削减医疗开支的过程中,我们该做的不是对健康人群加强疾病筛查,而是减少这类检测。以艾滋病为例,公共健康官员总是建议将有限的资源用在“刀刃”上,即用在男同性恋者、采取静脉注射的吸毒分子等高危人群身上。
一边开车一边发短信容易造成事故,但各州出台的禁止开车发短信的法律似乎并没有遏制这种行为。事实上,这些法律甚至有可能让情况变得更糟,因为司机在发短信时会想办法将手机藏得更为隐蔽,更加不把心思放在专心开车上。
拥有最佳信用记录的客户每个月总能准时付清账单,信用卡公司没法从他们身上赚得一点儿利息;那些账单数额巨大且经常忘记按时还款的客户才是信用卡公司的“金主”,高额的利息给公司带来了丰厚的利润,只要这些客户不违约就行。
第6章 蒙提·霍尔悖论
在《让我们做个交易》节目中,主持人打开的 3 号门后面是一头羊,在剩下的 7 号门和 2 号门中必定有一扇门后面是汽车 , 你应该如何选择才能中大奖?
“蒙提·霍尔悖论”是一个著名的概率难题。1963 年美国开播的电视游戏节目《让我们做个交易》中,参赛者们就会面临这个难题。正是这个亘古不变却又兴致盎然的悖论,让这类竞赛游戏长盛不衰,至今有许多国家的电视台依然在制作并播放类似的节目。记得读小学的时候一回家我就会打开电视观看《让我们做个交易》。这个节目给统计学家带来了巨大的惊喜。每一期节目播到最后,总会有一个参赛者脱颖而出,站在主持人蒙提·霍尔旁边,在他们的眼前有 3 扇巨大的门,编号分别为 1、2、3。蒙提会告知参赛者,其中的一扇门的门后摆放着极为诱人的大奖(比如说一辆小轿车),而另外两扇门的后面各站着一头羊,参赛者需要在这 3 扇门中选择一扇门,并获得那扇门后面的奖品。(如果有参赛者选中了羊,我怀疑他们是不是真的会把那头羊牵回家,因为在普通人看来,绝大多数参赛者都希望能开一辆新车回去。)游戏刚开始时,中大奖的概率一目了然,两头羊和一辆车,参赛者有 1/3 的概率选中那扇后面是轿车的大门。但正如之前提到的,这个节目及其主持人蒙提·霍尔之所以能够在美国概率学课本中占得一席之地,是因为这个节目还有一个精心的 安排。当参赛者选择了一扇门之后,蒙提会打开剩下的两扇门中的一扇,向观众和选手展示这扇门后面的奖品——一头羊,然后蒙提会再次询问参赛者是否要改变当初的选择,也就是在最初选择的那扇门和剩下的那扇门中再选择一次。
为了让表述更加清楚,我们假设参赛者最初选择的是 1 号门,蒙提随后打开了 3 号门,发现门后站着一头活羊。此时,场上还有两扇门是关着的,1 号门和 2 号门,如果小轿车藏在 1 号门的后面,那么参赛者就中奖了,如果小轿车藏在 2 号门的后面,参赛者就会与大奖失之交臂。但就在这个时候,蒙提并不急于揭晓答案,而是再次询问参赛者是否坚持原来的选择,如果参赛者改变主意了,就相当于放弃了一开始选的 1 号门,而改选 2 号门。记住,这两扇门此时依旧紧闭着。参赛者唯一得到的新信息是,在自己刚刚没有选择的那两扇门中,至少有一扇门的后面是一头羊。
参赛者应不应该改变最初的选择?
答案是肯定的。如果参赛者坚持最初的选择,那么中大奖的概率为 1/3, 如果改选剩下的那扇门,那么中奖的概率就是 2/3。如果你不相信的话,请往下读。
我承认这样的一个答案似乎有违直觉,因为在这个过程中,参赛者中大奖的概率似乎一直都是 1/3,不管这个参赛者后来有没有改变选择。一共有 3 扇关闭的大门,一开始的时候每一扇大门后面藏着大奖的概率都是 1/3,但是当参赛者改变自己最初的选择转而选择另一扇门之后,中奖的概率会随之变化吗?
问题的关键就在于,主持人蒙提·霍尔本人是知道每一扇门背后的奖品的。如果参赛者选择了 1 号门,而且恰好小轿车就在这扇门的门后,那么蒙提就可以在 2 号或 3 号门中随便选一扇门打开,向观众展示一头羊。
如果参赛者选择了 1 号门,而小轿车停在 2 号门后,那么蒙提就会打开 3 号门。
如果参赛者选择了 1 号门,而小轿车停在 3 号门后,那么蒙提就会打开 2 号门。
通过改变之前的选择,参赛者就能从两次选择中获益,好处自然要比一次选择多。为了说服大家,我会用 3 种不同的方法来证明这一分析的正确性。
第一种是从经验主义角度出发的。2008 年,《纽约时报》专栏作家约翰·泰拿尼专门就“蒙提·霍尔现象”写了一篇文章。随后这份报纸还在网站上开辟了一个互动专题,读者可以亲身体验这个游戏,包括提示你是否要改变选择,游戏的最后甚至还有可爱的小羊和小轿车从门后跳出来揭晓答案。这个游戏会记录下你改变和坚持最初选择的成功率,你可以试一下。我特地让我的小女儿玩了 100 次这个游戏,每次都在打开一扇有羊的门后改变最初的选择;然后又找她的哥哥玩了 100 次,全都坚持一开始的选择。我的女儿有 72 次中了大奖,儿子只中了 33 次。他们都从我这里获得了两美元的辛苦费。
《让我们做个交易》节目每期的统计结果也印证了这一点。《醉汉的脚步》的作者列纳德·蒙洛迪诺也证实,那些改变选择并得到大奖的参赛者人数是坚持最初选择并中奖的参赛者的两倍。
我的第二个解释是从直觉出发。假设游戏规则有变,首先参赛者会在 1、2、3 号门中挑选一扇,然后主持人蒙提在打开一扇门之前,问道“你是否愿意放弃你之前的选择,换取另外两扇门后面的奖品?”也就是说,如果你选择的是 1 号门,你可以放弃那扇门,从而获得 2 号和 3 号门后面的奖品;如果你选择的是 3 号门,你可以换成 1 号和 2 号门。
这并不是一个非常难作的决定。显而易见,你应该放弃一扇门换取两扇门,这样你中大奖的概率就从 1/3 上升到了 2/3。接下来,就是见证奇迹的时刻了:蒙提·霍尔在节目中展示一扇门后的羊,其实做的是相同的事情。一个最基本的道理,如果你能选择两扇门,那其中肯定有一扇门的门后是羊。主持人在问你是否要更换选择之前,打开了一扇门后有羊的门,实际上是为你做了一件大好事!他的言下之意就是,“你没有选的那两扇门有 2/3 的概率中大奖,而且你看,我已经帮你排除一扇门了!”
我们试想一下,假设你选择了 1 号门,蒙提接着问你是否要换成 2 号和 3 号门,然后你接受了,放弃一扇门换来两扇门,你此时得到轿车的概率也就上升为 2/3。而就在这个时候,蒙提打开了 3 号门——也就是你选择的两扇门中的一扇——发现门后是一头羊,你会有什么感受?是觉得自己中奖的希望变渺茫了?当然不是!如果轿车藏在 3 号门的后面,那么他打开的肯定会是 2 号门!蒙提可以说是什么都没干。
如果游戏正常进行,蒙提实际上是给你提供了两个选择,要么坚持最初选的那扇门,要么选择剩下的两扇门——只不过其中有一扇后面是羊的门被打开了,在这个过程中,蒙提还告诉了你另外两扇门中哪一扇门后面没有大奖,因此在如下的两种情况中你中大奖的概率是相同的:
- 先选择 1 号门,然后在任何一扇门打开之前同意换成 2 号和 3 号门。
- 先选择 1 号门,然后在蒙提打开有羊的 3 号门之后同意换成 2 号门(或者在蒙提打开有羊的 2 号门之后同意换成 3 号门)。
在这两种情况下,通过改变选择,你中奖的概率都由原来的一扇门增加到两扇门,因此你的赢面也从 1/3 上涨为 2/3。
我的第三种解释更像是第二种解释的极端版。假设摆在你面前的不是 3 扇门,而是 100 扇门。当你选择其中一扇门(比如说 47 号门)之后,蒙提·霍尔在剩下的 99 扇门中打开了 98 扇有羊的门,此时就剩两扇门没有打开了,一扇是你最初选择的 47 号门,一扇是蒙提剩下的(比如说 61 号门),你要换吗?
绝对要换!小轿车有 99% 的概率藏在你没有选的那 99 扇门的后面,而蒙提还好心地为你打开了其中的 98 扇门,他知道这 98 扇门的后面都没有小轿车。也就是说,如果你坚持最初的选择(47 号门),那么你开着小轿车回家的概率仅为 1%, 牵一头羊回家的概率却高达 99%; 如果你的最初选择是错误的,那么小轿车就肯定藏在另外一扇门后面(61 号门),如果你想中大奖,那就应该将最初的 47 号门换成最后剩下的 61 号门。
简言之,如果你有机会参加《让我们做个交易》节目,当蒙提·霍尔(或者是他的继任者)问你是否要改变选择时,你要毫不犹豫地点头。更夸张的说法是 , 这个例子告诉我们,你对概率的本能理解有时候会将你引入歧途。
第7章 黑天鹅事件
最不负责任的数据使用案例就是 2008 年金融危机爆发之前华尔街的风险评估机制了。那时候,整个美国金融行业使用的都是同一个风险晴雨表——风险价值(VaR)模型。理论上说,VaR 既是一个简洁的指标(将大量信息整合为一个单独的数字),又有强大的概率学支撑(对每家公司的资产和交易都给出了预期收益和损失值),是一个不可多得的投资工具。该模型认为,公司的每一项投资都存在着大量可能的结果,比如投资通用电气的股票,这些股票既有可能升值,也有可能贬值。如果在一个相对较短的周期内(比如一周)采用 VaR 模型进行投资评估,最有可能得到的结果是购入的股票在短期内基本维持原状,上涨或下跌 10% 的概率很小,上涨或下跌 25% 的概率就更小了,也就是说,变化越大,概率越小。
在分析了以往市场变动的数据之后,公司的数量分析专家会给出一个数字(比如说 1300 万美元),用来表示一项投资在一个特定周期内有可能让公司蒙受的最大损失,出现这种结果的概率为 1%。也就是说,这项投资在 99% 的情况下会使公司的损失低于 1300 万美元,但还有 1% 的概率造成重大损失。
请记住上一段内容里的最后一句话,这句话至关重要。
在 2008 年金融危机爆发之前,各大公司对 VaR 模型信任有加,在量化整体风险时都会采用这一统计模型。假设一个交易商手上有 923 项不同的“敞口头寸”(即可能会出现涨跌的投资),每一项投资都能像通用电气股票的例子那样进行 VaR 分析,然后再计算得出该交易商手中的证券组合的总体投资风险,该公式甚至还考虑到不同投资之间的相关性。例如,如果两项投资的预期回报呈负相关关系,即一项投资的损失会被另一项投资的收益所抵消,那么这两项投资的整体风险要小于其中任意一项投资。一般而言,投资部门的主管会知道其手下的交易员鲍勃•史密斯的 24 小时 VaR 为 1900 万美元,即在接下来的 24 个小时内,鲍勃最多会让公司亏损 1900 万美元,而且这一情况发生的概率仅为 1%。
更妙的是,该投资部门在任何时候都可以得出全公司的风险指数,只需要在上述基础上稍微向前推进一步即可。当然,这其中所包含的数学运算是非常复杂的,因为要考虑到公司所参与的种类繁多的金融产品,而且还涉及多国货币,每项投资的杠杆率(进行投资的贷款额)也不一样,不同国家的资金流动率也存在差别等。但这些都不能阻碍投资经理们在任何时候得出一个看上去十分精确的风险指数,正如《纽约时报》前财经作家乔·诺切拉所解释的那样,“VaR 最吸引人的地方,也是其最大的卖点就在于将风险描述为一个单一的数字——一个美元数据,仅此而已,而那些恰好不擅长数量分析的人就会趋之若鹜。”摩根大通公司是 VaR 模型的创始者,经过不断的开发和完善,每日的 VaR 如今已经有了一个新的名称——4:15 报告,因为在每天下午的 4 点 15 分,即当天的美国金融市场休市没多久,每一位公司高管的桌子上就都会出现 VaR 报告。
可是不幸的是,VaR 模型的风险档案里隐藏着两个巨大的问题。第一,模型构建的概率基础参照的是过去的市场行为,然而金融市场和啤酒盲品会不一样,前者的未来不一定是历史的重复,没有任何的理论证据可以保证 1980〜2005 年间的市场动态是 2005 年之后市场表现的最佳预测参照物。
第二,即使通过基本数据,我们能够借助 VaR 准确地预测未来风险,这 99% 的保证依然存在着失效的危险,因为真正把事情搞砸的正是剩下的 1%。
华尔街的数量分析专家们犯了 3 个最基本的错误。第一,他们混淆了“精确”和“准确”的概念。VaR 模型就像是我的高尔夫测距仪,我以为计量单位是“码”,可实际显示的计量单位却是“米”:确实精确,但并不准确。错误的精确让华尔街的高管们自以为是地认为他们对风险状况尽在掌握。第二,他们对基础概率的估算方式是错误的。正如之前格林斯潘在接受质询时所指出的,不应该只用 2005 年以前相对平稳和繁荣的经济数据来预测接下来几十年的市场表现。这就好像一个人去赌场玩轮盘赌,心里想着自己有 62% 的概率会赢,因为上次玩轮盘赌赢钱的概率就是 62%,结果怎么样呢?这对他来说将会是一个难熬、难忘的夜晚。第三,公司忽略了“尾部风险”,VaR 模型预测的是那些发生概率为 99% 的结果,这也是概率的工作原理(本书的后半部分将会不断地重复这一概念——即使是貌似不可能的事件,也有发生的可能。事实上,放眼望去,它们并没有人们想象得那样罕见,每天都有人被雷击中。)
本章接下来将会介绍一些最为常见的与概率有关的错误、误解和道德困境。
想当然地认为事件之间不存在联系。抛一次硬币得到正面的概率为 1/2,抛两次硬币结果都为正面的概率为 1/4,因为这两个事件是独立的,因此两次都得到正面的概率为各自概率的乘积。在领会了这一强大的概率学要点之后,你被正式提升为某大型航空公司的风险管理总监,你的助理告诉你越(大西)洋航班的引擎出现故障的概率为 10 万分之一,考虑到此类航班的班次较多,因此这样的风险还是应该极力避免。可喜的是,每一架越洋航班都配有至少两个引擎,你的助理计算得出在大西洋上空两个引擎都出现故障的概率为(1/100000)^2,即 100 亿分之一——一个理论上安全的风险。这个时候,你作为风险管理总监,就可以让你的助理收拾东西回家,以后再也不用来了。因为两个引擎发生故障并不是彼此独立的事件,如果飞机在起飞时迎面飞来一群天鹅,那么两个引擎都有可能出现损坏。同样的,许多其他的因素也会对飞机引擎的性能造成影响,如天气变化、维护不当等。如果一个引擎出现了故障,那么第二个引擎出现故障的概率肯定要大大高于 10 万分之一。
意识到这一点很难吗?对于 20 世纪 90 年代的英国检方来说,恐怕确实很困难,正是因为对概率的不当使用,他们做出了一次严重的司法误判。英国检方所犯的统计学错误正是想当然地认为几个不同事件之间是彼此独立的(跟抛硬币一样),而忽略了它们之间的联系(某个特定结果的出现会增加类似结果发生的可能性)。但这次的事件却是真实的,无辜的人因此蒙受了牢狱之灾。
人们犯的另一种常见错误是,面对相互独立的事件浑然不觉,甚至还将它们作为相关事件进行处理。假设你正在一家赌场里(虽然从统计学的角度看,你根本就不应该出现在这种地方),你会看到赌客们红着眼睛盯着骰子或扑克牌,嘴里念念有词“总该轮到我赢了吧”。如果轮盘球已经连续 5 次停在黑色区域了,有人就会想当然地认为下一次肯定会停在红色区域,大错特错!轮盘球停在红色区域的概率一直都没变,应该是 16/38,这就是“赌徒谬论”。
对于年龄区间在 14~26 岁的运动员来说,一次投篮命中和再次投篮命中之间的关联是负相关的。
检方谬误。假设你是法庭陪审团的一名成员,听到如下事实:(1)犯罪现场找到的 DNA 样本与被告的 DNA 相吻合;(2)除了被告以外,该 DNA 样本与其他人相吻合的概率为百万分之一(在这个例子中,我们姑且认为检方提供的概率是准确的)。在这些证据的基础上,你会认为被告人有罪吗?
但愿你投的不是赞成票。
当统计证据的存在背景遭到忽视时,检方谬误就成了不可避免的事实。下面的两个场景分别解释了 DNA 证据是如何被用来指证被告的。
被告一:该被告是被害人生前的恋人,但被后者抛弃,在离犯罪现场 3 个街区以外的地方被捕,身上携带着杀人工具。在被捕之后,法医从他身上强行提取了 DNA 样本,后被证实与犯罪现场的一根头发相吻合。
被告二:该被告于几年前在另一个州以相同的罪名遭到起诉。一个囊括 100 多万名暴力罪犯 DNA 信息的国家级数据库里恰好收集了该被告的 DNA 样本,警方在犯罪现场找到了一根头发,提取了其 DNA 信息并在这个数据库中进行自动比对,比对结果最终指向了这名被告,而根据调查,他与被害者并无任何关系。
正如之前所说的,在这两个案例中,检方都可以义正词严地宣称,犯罪现场找到的 DNA 样本与被告相吻合,且该 DNA 样本与除被告以外的第二人相吻合的概率仅为百万分之一。但是在第二个案例中,被告完全有可能就是那个“第二人”,即 100 多万名 DNA 信息所有者中恰好与真正的杀人凶手的 DNA 相似的那个人。这是因为通过 100 万次的数据库样本对比,找到“第二人”的概率相对提升了。
回归平均数(或趋均数回归)。你或许曾经听到过一个叫作“《体育画报》封面诅咒”的说法,即成为《体育画报》封面人物的运动员或团队,在之后比赛中的成绩会出现不同程度的下滑。一种解释是,成为该杂志的封面人物会对接下来的表现产生不利影响。而另一个在统计学上更加说得过去的解释是,能上杂志封面的通常都是那些近期表现尤为出色的运动员或队伍,如 20 连胜之类的异乎寻常的竞技 表现,而他们之后的比赛成绩只不过是回归正常水平,这一现象就叫作回归平均数。概率学告诉我们,跟在异常值——在某个方向上远离平均数的数据——之后的更有可能是那些接近(长期积累得出的)平均数的数据。
回归平均数现象可以用来解释为什么芝加哥小熊队总是花大笔的“冤枉钱”,请一些让球迷们失望的自由球员为其效力。通常,棒球运动员在完成了一个或两个成绩极佳的赛季之后,便获得了谈判加薪的资本,换上一身小熊队的球服并不一定会让这些球员的表现变差(虽然球员表现与球队的训练和管理十分有关),但是小熊队花了大价钱买来的却是这些超级明星超常发挥的“尾端”,每个球星超水平发挥的时间段都是有限的,也就是那么一两年,过了超水平发挥的时间之后,他们的表现便会趋于正常,这也是为什么他们在小熊队效力时会让球迷大失所望——并非因为他们的技术很差,只不过是正常水平而已。
同样的现象还可以用来解释为什么有些学生在考试中会超常发挥,有时候又会不尽如人意;有些学生明明考得没有平时好,但重考的成绩却又稍稍提升了。要解释这一回归现象,一种思路是学生的考试成绩(无论是文化课还是体育课)基本上是由个人的努力和运气(统计学家称之为“随机误差”)构成的。也就是说,那些在某次考试中超常发挥的学生只不过是交好运了,而那些考试成绩与平时相比大失水准的考生只是运气差了一些。当好运或厄运终于结束时(总有结束的那一天),随之而来的表现就会更加接近平均值。
乍一看,回归平均数可能会与“赌徒悖论”相排斥。当学生连续 6 次抛出的硬币都是反面朝上之后,下一次是不是“应该”正面朝上?他再次抛硬币得到正面向上的概率依旧没变:1/2。他已经连续多次抛出反面朝上的事实并不能增加他下一次抛出正面朝上的概率,每一次抛硬币都是一个独立事件。但是,我们可以期望接下来抛硬币的结果在总体上会和概率学所预测的一致,即半数是正面朝上、半数是反面朝上,而非之前出现的所有结果都是反面朝上。如果一个人一开始抛硬币的结果全都是反面朝上,那么在接下来的 10 次、20 次或 100 次抛硬币的过程中肯定会出现更多的正面朝上的情况。大数定律告诉我们,抛的次数越多,得到的结果就越接近平均值(如果情况相反,那我们就应该开始怀疑是不是有人作弊)。
最后还有一个有趣的情况,研究者们发现了一个《商业周刊》现象。当公司高管获得了备受瞩目的高级别奖项,包括被提名为《商业周刊》的“最佳经理人”,他们的公司会在接下来的 3 年内遭受利润和股价的双重下挫。但是与《体育画报》效应不同的是,这一现象要比回归平均数复杂得多。根据加利福尼亚大学伯克利分校和洛杉矶分校的两位经济学家乌尔里克·马尔门迪尔和杰弗瑞·塔特的研究,当公司 CEO 们坐到了“超级明星”的位置,他们会被自身的“光环”所影响。他们开始写回忆录,被邀请成为外部董事,甚至开始物色美女为自己的终身幸福作打算(其实两位经济学家只给出了前面两个解释,第三个解释是我自己加的,而且我觉得这个解释同样具有说服力)。马尔门迪尔和塔特写道:“我们的研究表明,媒体主导的超级明星文化会导致行为扭曲,而且扭曲程度要超过单纯的平均值回归。”换言之,如果某位 CEO 成为《商业周刊》封面人物,请马上抛售其公司的股票。
这样的一个政策乍看上去会让我觉得反感,因为政策制定者们似乎眼里只有政治的正确性,对其他一概视而不见。但仔细一想,我又对自己的立场没那么确定了。还记得之前介绍的有关预防犯罪的知识吗?在这个领域,概率学既可以给我们带来神奇,也会增添很多烦恼。通过概率模型,我们得知从墨西哥进入美国的冰毒贩毒者最有可能是年龄为 18〜30 岁、21 点至凌晨驾驶红色皮卡车的西班牙裔男子,但同时我们也知道符合上述标准的绝大多数西班牙裔男子都不是毒贩,那我们应该怎么办?这就是我在上一章描述得天花乱坠的预测分析方法的缺陷所在,至少是缺陷的一个方面。
统计性歧视。概率会告诉我们某个事件发生的可能性有多大,那么面对一个很有可能会发生的情况,我们到底应不应该做出反应?或者说,什么时候做出反应是可以的,而什么时候做出反应又是不可以的?2003 年,欧盟就业社会事务专员安娜·迪曼托波罗提出,保险公司的保费政策不得因为客户的性别不同而有所差别,因为这违反了欧盟的平等对待原则。然而,对于保险公司来说,以性别区分保费的做法仅仅是出于统计学的考虑,与性别歧视无关。男性的车险费用要高一些,这是因为他们出事故的情况较多;女性需要多缴纳养老保险,这是因为她们活的时间更久些。当然,有的女性发生交通事故的比例高于男性,有的男性活得比女性久,但正如上一章所提到的,保险公司并不关心这些,它们只关心统计学意义上的现实,因为只要它们把平均值弄对了,公司就会挣钱。对于欧盟委员会于 2012 年实施的禁止保费男女有别的政策,有趣的地方在于,相关部门并没有否认性别与保险所承担的风险之间存在关联,但它们只是一直在强调这一基于性别的保费差异是不可能接受的。
概率学告诉我们什么情况更有可能发生、什么情况更不可能发生,这仅仅是概率学的基础,也就是我们在之前几章里一直探讨的,但我们还不能忽视统计学的社会影响。如果我们想要捉拿暴力犯、恐怖分子、贩毒人员,以及其他有可能对社会造成巨大损害的个人,我们就必须动用手中的一切工具,概率只是其中的一种,如果在执法过程中死守着概率不放,而忽略了性别、年龄、种族、家庭、宗教以及国籍等综合因素,那将会犯下幼稚的错误。
对于这些信息(假设它们在某种程度上具有预测价值)的处理,我们能做什么、应该做什么将会是一个复杂的法律问题,而非单纯的统计问题。每天,我们都会收集到有关更多事物的信息,如果这些数据告诉我们正确的概率要比错误的概率高,我们是否就能堂而皇之地进行歧视了(这就是“统计性歧视”或“理性歧视”概念的由来)?那些会买鸟食的人逾期不还信用卡的概率较低(这是真的!),诸如此类的分析可以应用到生活的方方面面,但是分析应该做到哪种程度?如果我们建立一个能够识别毒贩的模型,正确率为 80%,那剩下的 20% 的无辜的人该怎么办?因为这些人将会无止境地遭到这一模型的骚扰。
摆在我们面前的一个更大的问题是,数据分析对人们的行为和事件结果的影响已经大大超出了分析人员的想象。对欧盟委员会禁止男女有别的保险费的决定,你可以表示赞成,也可以表示反对,但我可以保证这绝对不会是最后一个让人左右为难的决策。我们总是习惯性地认为数字是“冰冷、确凿的事实”,如果计算无误,那么我们就一定能够得到正确的答案。但一个更为纠结和危险的现实是,有时候正确无误的计算也会将我们带往一个危险、浮躁的方向:我们可以摧毁金融体系,也可以骚扰一个恰好在某个时间出现在某个街头的 22 岁白人男子,因为根据我们的统计模型,几乎可以确定他打算去买毒品。尽管概率有再多的简洁特性和精准优点,也不能替代人类作为行为主体对其所进行的计算、进行计算的原因所作的思考。
第8章 数据与偏见
2012 年春天,研究人员在权威杂志《科学》上刊登了一项惊人的发现。这项前沿研究表明,多次被雌性果蝇冷落的雄性果蝇也会“借酒消愁”。《纽约时报》头版对这项研究描述道:“这些急于成功的年轻雄性果绳,在面对一群心仪的雌性果蝇时一而再、再而三地遭受打击,结果它们和众多屡次被拒绝的成年男子一样,借助酒精来缓解内心无处释放的欲望。”
这一研究加深了我们对大脑奖赏系统的了解,从而更好地帮助我们在治疗药物和酒精依赖方面寻找新的治疗方法。一位医学专家将这项研究解读为“回到奖赏回路的起源,探究激发基本行为如性爱、进食和睡眠的原始动力”。
所谓纵向研究,就是对大量调查对象一生中不同时间点的信息进行收集,比如每两年进行一次采访。这类研究的参与者们会在长达 10 年、20 年甚至 50 年的时间里接受定期采访,积累下极为丰富的连续性信息。
但不是所有人在任何时候都能纵向研究,很多时候横向研究也是不错的选择,所谓的“横向数据集”即在同一时刻收集到的数据。例如,如果流行病学家正在寻找一种新型疾病(或某种已知疾病)的根源,他们可能会想到去收集所有病患的信息,希望能够从中发现规律:他们都吃了些什么?去过哪里?他们有什么共同点?与此同时,研究人员或许还会收集健康人的相关信息,以凸显两组对象之间的差别。
选择性偏见也会以其他方式呈现。一个针对某一机场消费者展开的调查肯定是存在偏见的,因为选择乘飞机出行的人一般来说会更加富有一些,而在 90 号州际公路旁的一个休息点展开的调查,可能会存在与机场调查结果相反的问题。此外,由于愿意在公共场合接受采访的人与不喜欢被打扰的人之间也是有差别的,因此这两个调查都有可能存在先天的偏见。假如你在一个公共场合询问 100 个人是否愿意接受一个小调查,其中有 60 人表示愿意回答你的问题,那么这 60 人与剩下的那些匆匆经过你身边、拒绝跟你有眼神接触的 40 人之间,可能在某些方面存在着巨大差别。
当样本中的个人主动提出要加入治疗组时,就出现了偏见的另一种形式,我们称为选择性偏见。例如,主动提出加入戒毒组的犯人与其他犯人是不同的,因为他们是主动要求加入这个组别的。即使通过跟进,发现戒毒组的成员在出狱之后再次人狱的概率要比没有参加戒毒组的犯人小,也丝毫不能证明戒毒组的存在价值。这些曾经的囚犯已经洗心革面地开始了全新的人生,我们可以说这是因为他们参加了戒毒组,但也有可能是因为其他因素恰好导致其有了主动申请加入戒毒组的愿望(比如产生了再也不想回到监狱的强烈欲望)。我们无法分离其中一种可能(戒毒组项目)与其他可能(成为一个主动申请加入戒毒项目的人)之间的因果关系。
记忆性偏见。回忆确实很神奇,但并不是优质数据的可靠来源。我们总是认为现在和过去是有逻辑联系的——有因才有果,这符合人类的思考方式。但问题是,当我们试图解释当前一些特别好或特别坏的结果时,我们的记忆便会出现“系统脆弱”的尴尬。1993 年,一位哈佛大学的研究人员进行了一项关于饮食习惯和癌症关系的研究,他收集了两组女性的饮食习惯数据,一组对象为被诊断出患有乳腺癌的女性,另一组对象则由年龄相仿的健康女性组成,通过对她们早年的饮食习惯进行对比研究发现:患有乳腺癌的女性在年轻时喜欢吃高脂肪含量食物的人数明显偏多。
但实际上,这项研究并不能揭示饮食习惯和癌症之间的关系,仅仅只是告诉我们癌症是如何影响一个女人对她早期饮食习惯的记忆的。所有参与研究的女性在 几年前都接受了一个关于饮食习惯的调查,那时她们中间还没有一个人被诊断出患有癌症。一个令人震惊的发现是,患有乳腺癌的女性在回忆她们的饮食构成时,食物的脂肪含量明显上升了,甚至比她实际摄入的要高得多;而没有患上乳腺癌的女性则没有这一倾向。《纽约时报》是如此形容这一记忆性偏见的“阴险本质”的:
一纸乳腺癌的诊断书不仅改变了一个女性的现在和未来,还改变了她的过去。患有乳腺癌的女性(无意识地)认为摄取过多高脂肪含量食物的饮食习惯极有可能是她们患病的罪魁祸首,因此她们的记忆(无意识地)认为自己过去摄入了太多高脂肪含量的食物。了解这一疾病历史的人,对于这样的一种思维方式是再熟悉不过了:这些女性与千万女性一样,不断回忆过去想要从中找到一个患病原因,然后再将这个原因植入记忆。
没有记忆性偏见是纵向研究优于横向研究的一个方面。纵向研究的数据都是基于当前收集的,当研究对象 5 岁的时候,我们会问他对于上学的看法,13 年之后,我们可以对其进行回访,看看他是不是从高中辍学了。横向研究的所有数据都是在某一个时间点上截取的,我们只能问一个 18 岁的高中缀学生当他 5 岁的时候对于上学持哪种态度,这位研究对象的回答必然没有 13 年前那么可靠和真实。
传统意义上的共同基金公司一般都会怎么做呢?操纵数据是永远的“救心丸”!下面就来说说,它们是如何在没有跑赢市场的情况下“跑赢市场”的。某家大型共同基金公司会同时开放许多只共同基金(有专家专门负责挑选股票,通常会有一个特定的关注点或策略),举个例子,假设一家共同基金公司开放了 20 只新基金,其中每只基金跑赢标准普尔 500 指数的概率都约为 50%(这一假设与长期数据是吻合的)。现在,基础概率学告诉我们,该公司第一年只有 10 只新基金的表现能够打败标准普尔 500 指数,连续两年打败标准普尔 500 指数的基金为 5 只,连续 3 年打败标准普尔 500 指数的基金只剩下了 2〜3 只。
最精彩的内容马上就要来了。届时,那些相比标准普尔 500 指数收益率不够理想的共同基金基本上都已经被悄无声息地关闭了(它们的剩余资产都被并入其他现有的基金中)。该公司接下来就可以大肆打广告,宣传这两三只“表现始终优于标准普尔 500 指数”的基金了,而实际上,它们在这 3 年的良好表现就相当于连续抛 3 次硬币都得到正面朝上的结果一样。它们接下来的表现很有可能会回归平均值,但此时投资者的钱已经被成功地骗进来了。真正能够在相当长一段时间里,对标准普尔 500 指数保持不败战绩的共同基金或投资专家少得可怜。
第9章 中心极限定理
我们通过对一家禽肉加工厂生产的 100 块鸡胸肉进行沙门氏菌检测,就能得出这家工厂的所有肉类产品是否安全的结论。这些“一概而论”的强大能力,来自中心极限定理。
使用样本对一个更大的数量对象进行推理(比如民意调查或是沙门氏菌检测)。
中心极限定理的核心要义就是,一个大型样本的正确抽样与其所代表的群体存在相似关系。当然,每个样本之间肯定会存在差异(比如前往马拉松起点的这么多辆客车,每辆客车乘客的组成都不可能完全相同),但是任一样本与整体之间存在巨大差异的概率是较低的。
在 99% 的情况下,任何一辆随机安排的客车上的选手的平均体重,都将会在全体运动员平均体重 ±9 磅的范围之内。
这些乘客的平均体重高于全体马拉松运动员平均体重整整 21 磅,只有低于 1% 的概率是马拉松运动员。因此,我可以有 99% 的把握认为这不是那辆失踪的马拉松客车,也就是说,我可以预期我的推理有 99% 的胜算。
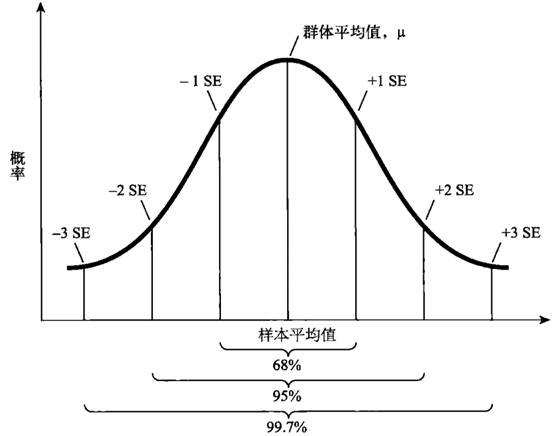
根据中心极限定理,任意一个群体的样本平均值都会围绕在该群体的整体平均值周围,并且呈正态分布。
中心极限定理通过对不同样本平均值出现概率的描述,能够让我们推理出更为深入的结论。在这个例子中,样本平均值将会围绕着群体平均值(也就是 7.09 万美元)形成一条正态分布曲线。记住,群体本身的分布形态并不重要,美国家庭收入的分布曲线并非正态分布,但样本平均值的分布曲线却是正态分布。如果我们连续抽取 100 次包含 1000 个家庭的样本,并将它们的平均值的出现频率在坐标轴上标出,那么我们基本可以确定在 7.09 万美元周围将会呈现一个熟悉的“铁钟”曲线分布。
正态分布曲线的过人之处就在于,能够大体确定有多少比例的数值位于整体平均值的一个标准差之内(68%),有多少数值位于两个标准差之内(95%),以此类推。
标准误差被用来衡量样本平均值的离散性。我们如何评价样本平均值在群体平均值周围的聚集程度?为了避免混淆,我们首先需要对两个概念进行区分:标准差和标准误差。关于这两个概念,我们有必要记住的是:
- 标准差是用来衡量群体中所有个体的离散性。在之前的例子中,标准差衡量的是弗雷明汉心脏研究中所有参与者的体重分布,或马拉松比赛中所有参赛运动员的体重分布。
标准误差就是所有样本平均值的标准差。
由于样本平均值是呈正态分布的(这一点要归功于中心极限定理),我们便可以通过这条神奇的曲线来获得推理所需的“超能力”。已知的是,差不多有 68% 的样本平均值会在群体平均值一个标准误差的范围之内,有 95% 的样本平均值会在群体平均值的两个标准误差的范围之内,有 99.7% 的样本平均值会在群体平均值 3 个标准误差的范围之内。
为了能够让中心极限定理成立,样本数量必须足够多(依照经验至少有 30 个);如果我们想要假设群体的标准差等同于样本的标准差,那么更要保证样本数量足够多了。
- 如果你从某个研究群体中多次随机抽取数量足够多的样本,那么这些样本的平均值会以整体平均值为中心呈现正态分布(不论该群体自身的分布情况是怎样的)。
- 绝大多数的样本平均值都会紧紧围绕在整体平均值的周围,通过计算标准误差就可以知道这些样本平均值到底是离得“近”还是“远”。
- 通过中心极限定理,我们便可知道样本平均值与整体平均值之间的距离及其概率。样本平均值离整体平均值两个标准误差的概率相对较低,3 个或以上标准误差的概率基本上为零。
- 如果出现了某个概率较低的结果,我们便可以推测是不是有一些其他因素介入,而且概率越低,其他因素介入的可能性就越大。
这些基本上囊括了统计推断的所有内容,而中心极限定理是让这一切发生的重要推动力。
第10章 统计推断与假设检验
我的统计学老师把我叫到了他的办公室,隐约记得他说过“你的期末考试成绩比起你的期中考试成绩有了很大的提高”之类的话,但丝毫听不出有任何夸奖的意味,从始至终我心里都感觉不太舒服,觉得老师话中有话,因为他一直在问我到底是怎么做到的,言外之意就是他怀疑我作弊了。现在做了多年老师的我,也终于能体会他那时的想法了,在我教过的所有课程里,几乎所有学生的期中成绩和期末成绩都有着极为显着的相关性。如果某一个学生的期中考试成绩在班上处于中等偏下的水平,而在期末考试中却一举成为班上的佼佼者,这是一件非常不寻常的事。
我当时的解释是,我提早完成了论文,而且开始重视这门课程(认真阅读了课本,并完成了老师布置的课后作业),他看上去似乎对我的回答感到较为满意。我随后离开了他的办公室,但还是被他的含蓄“指控”搅得心神不宁。
说出来你们可能不信,通过这么一个小插曲,我们就可以窥见统计推断的优劣。统计学无法确凿地证明任何东西。与之相反,统计推断的力量在于:先发现一些规律和结果,然后再利用概率来证明这些结果的背后最有可能的原因。
有时候最有可能的解释并非正确的解释,极端罕见的事情总会发生。
南加利福尼亚州的一位名叫琳达·库珀的女士被闪电击中了 4 次。据美国联邦应急管理局披露的统计数字,被闪电击中一次的概率只有 60 万分之一。
(1)假如试验药物没有疗效,则治疗组和对照组之间几乎没有可能会出现如此巨大的差距。(2)因此,试验药物没有积极疗效的可能性很小。(3)那么结论(2)的反面,也就是试验药物具有积极疗效的可能性较大,并且恰巧能解释对照试验的数据结果。
统计推断过程中最常使用的工具之一就是“假设检验”。
说服法官或陪审团来推翻一开始的无罪假设,并接受其反面事实,即被告有罪。从逻辑学来看,如果我们能够证明某个零假设不成立,那么其对立假设(又称备择假设)肯定为真。下面举一个例子。
零假设:某种新药在预防疟疾方面并没有比安慰剂更加有效。
对立假设:该新药能够帮助预防疟疾。
数据:随机选取一个小组服用新药,另一个小组作为对照组服用安慰剂。一段时间过后,服用新药的小组的疟疾发病率要远低于对照组。如果该新药不具备任何疗效,那么出现这一结果的概率是非常低的。因此,我们推翻该新药没有疗效的零假设,承认其对立假设成立,即该新药能够帮助预防疟疾。
零假设和对立假设在逻辑方面是互补的,也就是说,如果其中一个假设为真,则另一个假设为假;如果我们推翻了其中一个假设,那就必须承认另一个假设。
研究人员经常会提出一个零假设并希望有朝一日能够推翻它,虽然这听上去有违直觉。在上面的两个例子中,研究的“成功”(寻找到一种新的治疗疟疾的药物以及减少重新犯罪率)都意味着推翻零假设,而真正通过数据做到的只有第一个例子。
在法庭上,推翻无罪假设的最基本条件是通过定性分析,“在不存在任何疑义的前提下认定被告有罪”,至于法官或陪审团如何理解这句话,那就因人而异了。基本上统计学也是这个道理,但在“排除疑义并定罪”的过程中用到了定量分析。研究人员最常提出的疑问是,如果零假设成立,那么完全是出于巧合的概率有多大?以此类推,医学研究人员会问,如果这一试验药物对治疗心脏病无效(也就是零假设), 那么治疗组有 91% 的病人病情好转且对照组仅有 49% 的病人病情好转的概率有多大?假如数据显示零假设基本上不可能成立,比如上述的医学例子,那么我们必须推翻它,并承认其备择假设(该药物对治疗心脏病有作用)成立。
零假设到底要有多“不合情理”才能让我们将其推翻,并承认其反面假设为真?
研究人员推翻零假设最常参考的“门槛”之一是 5%,经常以十进位小数的形式表示为 0.05。如果一个零假设想要为真,其支撑数据的结果必须至少达到 0.05 这个显着性水平,才能保证该假设具有意义。
患有自闭症谱群疾病的孩子的大脑在生理结构上与其他孩子有什么不同吗?如果回答是肯定的,那么将有助于研究人员更好地理解自闭症的发病原理,从而为自闭症的治疗和预防提供新的信息。
问题是:仅凭一项样本规模并不是太大的研究(只有 59 位自闭症儿童,健康儿童的数量更少,仅为 38 位),我们就能推而广之地认为所有患有自闭症谱群疾病的儿童的脑量都异于常人吗?回答是肯定的。研究人员总结道,在儿童的脑量与患自闭症无关的前提下,两组样本(59 位自闭症儿童和 38 位健康儿童)的脑量出现如此差异的概率只有千分之二(p=0.002)。
我还特地找到了那期《普通精神医学纪要》,翻看了论文原文。里面的研究人员所采用的方法并没有比截至目前我们所学的概念更复杂,接下来,我将为大家大致介绍一下这篇在社会影响力方面和统计学意义上都非常重要的论文。首先你应该认识到,研究中的两组孩子 59 位自闭症患儿和 38 位健康孩子——能够合理地代表他们所在的群体,而且样本数量足够了,因此适用于中心极限定理。如果你早已将上一章的内容忘得差不多了,没关系,我们先来简单复习一下:(1)任意一个群体的样本平均值将会在群体平均值周围呈正态分布(⑵样本的平均值和标准差约等于所在群体的整体平均值和标准差;(3)约有 68% 的样本平均值位于群体平均值一个标准误差以内,约有 95% 的样本平均值位于群体平均值两个标准误差以内,以此类推。
如果用通俗的语言来总结上述 3 点内容,就是任何一个样本与其所代表的群体之间应该具有相似性;虽然每个样本都是不同的,但任何一个正确抽取的样本的平均值与整体平均值相差甚大的概率相对来说都是非常小的。同样的,我们可以预测,取自相同群体的两个样本彼此之间也应该差不多。在此基础上我们换个角度思考,如果两个样本的平均值相差甚远,那么最有可能的解释就是它们来自于不同的群体。
那份关于自闭症的研究论文所用的基本方法论是一样的。研究人员将两组孩子的几次大脑检测结果进行了比较(孩子在 2~5 岁通过核磁共振成像分别对大脑进行一次检测)。我们现在只看其中的一项指标——总脑量。研究人员的零假设大致上是:无论孩子有没有自闭症,他们的大脑在解剖学上都没有什么差别。备择假设为:患有自闭症谱群疾病的儿童,他们的大脑与健康儿童的大脑有根本性的不同。像这样的一个研究发现自然会存在许多问题,但至少为未来的自闭症研究和探索提供了一个方向。
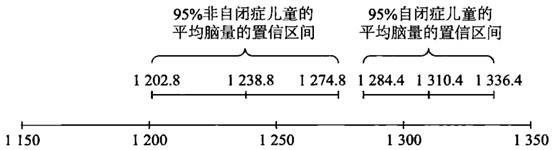
在该研究中,自闭症儿童的平均脑量为 1310.4 立方厘米,对照组儿童的平均脑量为 1238.8 立方厘米,所以两组儿童的平均脑量之差为 71.6 立方厘米。假如自闭症跟儿童的平均脑量并无任何关系,那么出现这一结果的概率有多大?
如果你还记得上一章的内容,就会很自然地想到我们可以先求出样本的标准误差:s/fa, 其中 8 为样本的标准差,n 为样本数量。研究为我们提供了这些数据:自闭症组中 59 位儿童脑量的标准误差为 13 立方厘米;对照组中 38 位健康儿童脑量的标准误差为 18 立方厘米。你应该还记得中心极限定理告诉我们,有 95% 的样本平均值会落在整体平均值左右两个标准误差的范围内。
因此,我们可以从手中的样本推断出,所有自闭症儿童的平均脑量在 1310.4±26 立方厘米范围内的概率为 95%,在统计学上我们称之为置信区间。我们可以有 95% 的把握声称,在 1284.4〜1336.4 立方厘米的置信区间里包含了广义上所有患自闭症谱群疾病的儿童的平均脑量。
用同样的方法,我们也能够有 95% 的把握声称,在 1238.8 土 36 立方厘米的范围内,也就是 1202.8~1274.8 立方厘米的置信区间里,包含了所有非自闭症儿童的平均脑量。
我承认,上面出现了很多数字,或许烦躁的你刚刚已经将这本书扔到了角落里。假如你没有做出这么冲动的事情,或者你又走过去把书捡了起来,那么你就应该会发现,这两个置信区间居然没有重合的地方。自闭症儿童的平均脑量所处的置信区间的最小值(1284.4 立方厘米),依然要高于非自闭症儿童平均脑量所处的置信区间的最大值(1274.8 立方厘米),请看下面的图解。
这可能是证明自闭症儿童的大脑,的确存在解剖学差异的第一条线索。是的,照目前来看,这只能算是一条线索,因为我们所有的推断都是建立在不到 100 位儿童组成的样本的基础上,或许我们只是遇上了比较特殊的样本。
假设自闭症儿童和健康儿童的脑量真的不存在任何解剖学上的差别,即他们属于同一个群体,那么两组样本出现如此巨大差距(一个是 1310.4 立方厘米,一个是 1238.8 立方厘米)的准确概率有多少?我们可以算出已知平均值差异的假定值。
100 位 NBA 球员并计算出他们的平均身高为 6 英尺 7 英寸(约 2.01 米),那么另外再随机抽取 100 位 NBA 球员,他们的平均身高也应该接近 6 英尺 7 英寸。好吧,或许这两组样本之间会存在一两英寸的差别,但存在 4 英寸差别的概率就没有那么大了,相差 6~8 英寸的概率可以说是微乎其微。我们可以计算出两个样本平均值之间差异的标准误差,通过这个标准误差,以及不同样本平均值之间的差距,我们可以判断样本平均值的离散程度。重要的是,我们可以通过这一标准误差计算出两个样本来自同一个群体的概率。以下就是具体流程:
- 假如两个样本均抽取自同一个群体,那么最好的结果是它们的平均值之差为零。
- 中心极限定理告诉我们,在重复抽取的样本群里,两个平均值(样本平均值与群体平均值)之间的差将会呈正态分布。(承认吧,你是不是开始有点爱上中心极限定理了?)3. 假如两个样本真的来自于同一个群体,那么有 68% 的概率,两个平均值之间的差小于一个标准误差;有约 95% 的概率,这个差会处于两个标准误差以内;有 99.7% 的概率会处于 3 个标准误差以内。这就是那篇自闭症研究论文的结论落脚点。
如前文所述,自闭症儿童组和对照组的平均脑量之差为 71.6 立方厘米,标准误差为 22.7, 也就是说,两组样本的平均值之差超过 3 个标准误差,我们能够据此计算出,如果这两个样本真的来自于同一个群体,那么出现如此极端结果的概率只有千分之二。
在统计推断的巨大光环之下,我们也要小心它的陷阱。
一在没有作弊的情况下。因此,对于任何一类假设检验来说,我们都面临一个根本性的两难困境。
第11章 民意测验与误差幅度
每一个拨出去的号码都应该有一位对应的成年人接听,但如何选取也应该有一个“随机的程序”,如要求让当前家中年纪最小的成年人来回答问题。这一个程序经过优化,能够让接听人的年龄、性别比例更加接近真实的成年人口。最重要的是,调查人员会尝试在一天的不同时刻拨打电话,以确保被挑中的电话号码能够打通。这些不断重复的操作一包括重拨某个电话多达 10 多遍——都是获得一个平衡样本不可缺少的重要组成部分。如果只是在工作时间随机拨打电话,能打通最好,打不通就更换其他号码,直到凑齐所需的样本数量,这样做当然在操作上更加容易实现,也更省钱,但这样的一个样本很有可能会存在偏差,在家接听电话的人很有可能大多是失业者或老人等。如果你只是想证明民意测验结果是美国总统奥巴马在失业人口、老人以及热心接听陌生来电人群中的支持率为 46% 的话,那你这样做是可以的。
检验民意测验是否正确有效的另一个指标是:被选中的电话号码中有多少接听者最终能够完成电话调查?假如完成率很低,那么就要小心会出现样本偏见了。不接受电话调查的人越多,或者家中电话一直处于无人接听的状态,那么这些人就越有可能与那些完成调查的人存在本质区别。民调策划人可以通过分析那些无法联系上的电话用户的已知信息来决定是否存在“无应答偏见”,这些人是否都住在同一个地区?他们拒绝采访的原因是不是都是类似的?他们是不是大多来自同一个种族、民族或收入群体?通过此类分析,我们便能够知道较低的回应率是否会影响到某次民意测验的结果。
2002 年起,每年的民意测试都显示有超过 60% 的美国人支持对谋杀犯判处死刑。美国人对死刑判决的支持率一直在一个很小的范围内变动,最高时的支持率为 2003 年的 70%, 其他时候支持率也曾低至 64%。但民调数据的结果是很清楚的:大多数美国人都支持死刑。
事实是这样的吗?当把无假释终身监禁作为选项放人问题中去之后,美国人对于死刑的支持率就大大下降了。2006 年的盖洛普民调发现,只有 47% 的美国人认为对谋杀犯判处死刑是合适的,而有 48% 的受访者选择了终身监禁。这可并非某场晚宴上的统计学玩笑,这意味着当无假释终身监禁作为一个可靠的选择时,多数美国人将不再支持死刑。在作公众调查的过程中,问题的设置以及提问的方式都会对结果产生巨大影响。
政客们就常常利用这一点来获得对自己有利的民调结果。例如,选民们对“免税”一词的好感度就高于“减税”,其实这两个词说的是同一个含义。同样的,相比起“气候变化”,选民们更加关心“全球变暖”,虽然后者只是前者的形式之一。政客们总是通过非中性词的使用来操纵选民的反应。如果一个中立、正直的民调机构想要获得正确有效的结果,它们必须警惕那些可能会影响反馈信息准确性的用语。
像盖洛普这样的机构会经常组织开展“分离样本测试”,也就是将同一个问题的不同问法用在不同的样本人群里,以便判断用词上的小小变化到底会不会影响回应者的答案。对于盖洛普民调机构专家弗兰克·纽波特而言,每一个问题的答案都是有意义的数据,就连那些看上去似乎有些矛盾的答案也不例外。美国人对于死刑的态度在终身监禁的刑罚颁布之后发生了剧烈改变,这其中就透露了一些重要的信息。纽波特说,关键在于要在一个大背景下看待民意测验的结果。对于一个复杂的话题,只看一个问题或一次民调结果是不可能完全看透公众的心理的,此时更需要有大局观和联想力。
受访者说的就一定是真的吗?民意测验就像是网恋,在对方所提供的信息里总是有那么一点儿“言不由衷”的成分。我们都知道,人都有撒谎的时候,尤其是当问题比较尴尬或敏感时。
选举民调尤其关键的一步是,将那些不会在选举日当天去投票站投票的美国公民筛选出来(因为如果我们想预测某次选举的胜利者,那么那些不打算去投票的人的观点对于我们来说就是无关紧要的)。作为个人而言,他们总是会说自己会去投票,因为他们觉得这是民调公司愿意听到的答案。但是有研究表明,那些自称会去投票的人中有 1/4〜1/3 的人最终没有投票。为了减小这类抽样偏见对民调结果的影响,一种方法是向受访者提问他们是否参加了上一次或前几次的选举投票,那些每场投票都参加的受访者最有可能在未来的选举中投票。如果担心受访者会羞于表达某个社会接受度不高的观点,例如对某个激进组织或民族群体的负面印象,民调人员会采用迂回的问法,如“你身边有认识的人”持有这种观点吗?
调查结论中的那句 “调查的准确性保证结论能够代表全体美国成年人的性行为”是建立在两个前提之上的,受访者是从全体美国成年人中正确抽取的样本,受访者提供了诚实准确的答案。
民意测验真正的挑战有两个:设计并选取正确的样本 > 用恰当的方式从该样本中获取合适的信息,以准确地反映他们的真实感受。
第12章 回归分析与线性关系
工作压力过大会致人死亡吗?答案是肯定的,有大量证据表明工作压力会导致早逝,尤其使心脏病猝死的概率陆增。但这种致命的压力或许跟你想象的有所不同。公司高管们几乎每天都要做出重要决策,这些决策关系到他们公司的前途命运,但他们所承受的风险要远远小于他们的秘书,后者必须兢兢业业地接听电话,完成上级布置的各种任务。但这怎么可能呢?其实最危险的一类工作压力来自于对自己的工作任务“缺乏控制力”。针对数千名英国公务员的多项调查(“白厅”研究)发现,那些对自己的工作没有支配能力的雇员——也就是基本上对干什么、怎么干没有话语权的人——相比起那些拥有更多决策权的雇员来说,前者的死亡率更高。由此表明,并不是那些“权力越大,责任也越大”的压力置你于死地,而是那种等着上司给你布置任务,但自己又没有权力决定怎么完成、何时完成这些任务的压力把人压垮了。
一个简单的相关关系,并不足以让人得出某类工作对健康有害的结论。在发现了英国政府系统中低级别的雇员更容易患上心脏病之后,我们还必须考虑到其他可能的因素。例如,我们可以想见这些低级别雇员的受教育水平要比高层官员们低;这些人更有可能染上烟瘾(或许是因为他们在工作中郁郁不得志);低级别雇员小时候的体质较弱,从而影响了长大后的工作前景;又或者较低的收入使得他们无法享受到好的医疗资源等。重点在于,任何一项只是简单地比较某个大型人群中个体(或不同人群)健康状况的研究都不会告诉我们太多有用的结论,在这样庞杂的数据中有太多的干扰因素会模糊我们对那些真正值得注意的关系的看法。心脏病真的是“低级别工作”导致的吗?又或者只是这类雇员所共有的一些因素共同导致的?如果我们认同了后者,那就等于完全无视一个真正的公共健康威胁。
如果处理得当,回归分析能够排除其他因素的影响
如果将统计学的基本概率门槛设定为 5%,那么这一个发现就具有了统计学意义。
让我们先好好思考一下上述这个例子。假设这项研究对比的是一群定期打壁球的人和一群从不运动的人——两类人的体重相当。打壁球的确对增强心脏功能有好处,但是,我们也不能忽略壁球这种运动并不是一般人能长期消费得起的,那些有打壁球习惯的人通常是社会的上流人士,他们加入的一些俱乐部常常有壁球场地供他们使用。同时,富有的人所能接触到的医疗资源自然更为丰富,这也有利于他们保持心脏健康。如果研究人员想草草了事,当然可以将这些人的心脏健康归功于打壁球,但事实上真正的健康受益于足够支撑壁球运动习惯的财富(打马球也是相同的道理,有人说参与马球运动的人更健康,其实这也是财富和优质医疗的功劳,不用想都知道打马球的过程中真正锻炼了身体的主要是马)。
还有可能是因果关系倒置,会不会是拥有了健康的身体才更愿意运动呢?当然有可能。那些体弱多病的人,尤其是心脏有先天性缺陷的人不宜从事剧烈运动,他们不大可能定期去打壁球。但如果研究分析过于敷衍和简单化,就会说运动有益于身体健康,而实际上却是那些天生身体不好的人不经常从事运动。照这个观点,打壁球并没有让任何人变得更健康,而只不过是将健康的人与体质差的人区分开罢了。
回归分析的强大能力表现在:将我们所关心的统计关联隔离出来,如工作中的支配力和心脏病,同时还不忘考虑其他可能会对这一相关关系产生影响的因素。
具体是如何做到的呢?如果我们得知英国政府中低级别雇员的身体要比他们上司的体质更弱,那我们怎么确定在心血管健康状况不佳的致病原因里,有多少比例源于他们低级别的工作,多少比例因为吸烟?这两个因素看上去似乎是彼此缠绕、密不可分的。
通过回归分析就能将它们解开。为了让大家都能理解其中的奥妙,我必须从基础说起,无论是哪种形式的回归分析——从最简单的统计学关联到诺贝尔奖获得者搭建的复杂模型,都离不开的基本概念。最核心的一点是,回归分析寻找的是两个变量之间的最佳拟合线性关系。举个简单的例子,身高和体重的关系。虽然不是绝对的,但身高较高的人一般体重应该更重。我们将一组大学毕业生的身高和体重标记在坐标轴上,不知道你会不会回忆起我们在前文中讲过的内容。
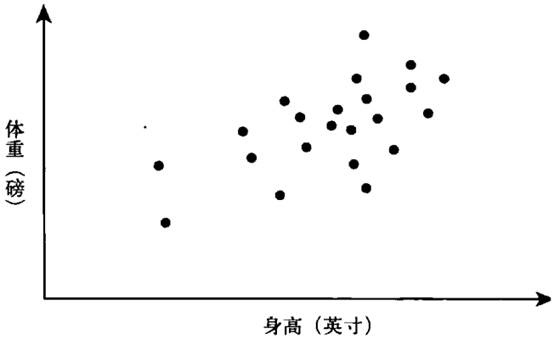
如果让你描述一下上面的图,你或许会说“体重看上去似乎随着身高的增加而增大”之类的话,说得很对,但离满分还有点距离。回归分析能够让我们更进一步,用更加精确的话语来描述这两个变量之间的线性关系。
大致来看,符合身高和体重数据趋势的线有很多条,但我们如何知道哪一条才是“最佳”的?我们又如何定义“最佳”这两个字?回归分析的一个常用方法为最小二乘法(OLS), 为什么 OLS 能够得出最佳拟合线性关系,我们留给更高阶的课本去解释,这里的关键点在于,OLS 直线可以让所有数据的残差平方和为最小。
对于任意一个回归系数,我们只需要关心 3 件事情就行了:正负、大小和含义。
正负。回归系数的正负揭示了自变量与因变量之间相关关系的方向。
大小。自变量到底能对因变量产生多大的影响?这种影响会达到何种程度?在上述例子中,每英寸身高都关系着 4.5 磅的体重,而 4.5 磅对于一个人的体重来说是一个不小的重量。在解释一些人为什么比另一些人的体重更重时,身高自然是一个重要的因素。
一口洁白的牙齿与每年多挣 86 美元之间存在相关关系。
但是,那又怎么样?我们的确发现了一个具有统计学意义的现象,但从社会学角度来看它其实无关紧要。首先,86 美元并不是一笔足以改变人生的金钱,在公共政策制定者的眼里,86 美元或许还不够每年牙齿美容的费用,因此我们甚至无法向年轻雇员推荐这类投资。此外,虽然下一章的内容会着重讲解回归分析中的陷阱,但我还是忍不住想要就方法论这方面的内容先说几句。例如,拥有完美的牙齿很有可能与本人的性格特点有关,正是因为这种性格特点,才带来了更高的收入,他们之所以挣得比别人多,是因为他们具备爱护牙齿这种性格,而非牙齿本身。这个例子告诉我们,要时刻关注解释变量与我们所关心的结果之间相关关系的大小。
3000 名美国成年人进行身高和体重数据的收集,那么在回归分析中我们可能会发现,他们平均身高每增高 1 英寸,相应的体重增加值为 4.3 磅;如果重复抽样和计算,那么每英寸身高所对应的体重增加值有可能变成 5.2 磅。正态分布又一次成为我们的朋友。
但是,我必须警告你的是,对于小型样本数据(例如 20 位成年人而非“变化的一生”项目的 3000 人)来说,正态分布将不再是我们的“好朋友”。具体来说,假如我们对不同的小型样本进行回归分析,就不能指望这些回归系数会围绕着全体美国成年人身高和体重的真实情况呈正态分布,此时的分布情况我们称为“t 分布”(简单概括之,t 分布比起正态分布来说更加分散,因此左右两条“尾巴”的幅度更大)。
一旦得出了回归系数和标准误差,我们便能对“解释变量和因变量之间没有相关关系(即回归系数为 0)”的零假设进行检验了。
在上述有关身高和体重的简单例子中,假如对于全体人口来说身高和体重并不存在任何相关关系,那么我们在“变化的一生”样本中得出每英寸身高对应 4.5 磅体重的概率有多高?我在电脑上用一款最基础的统计软件进行了回归运算,得出身高系数的标准误差为 0.13, 也就是说,如果我们重复此分析,比如说有 100 个不同的样本,那么预计将会有约 95 个回归系数落在人口真实参数两个标准误差的范围内。
由此,我们可以用两种不同但彼此相关的方式呈现这一结果。第一种方式是,我们可以建立一个 95% 的置信区间(4.5±0.26),也就是说,在 95% 的情况下回归系数会落在此区间里,也就是 4.24~4.76 之间,用基本的统计软件就能算出这一区间。第二种方式是,我们可以说在身高和体重的相关性 95% 的置信区间里不包括零。由此,我们就能有 95% 的把握推翻“身高与体重之间不存在相关关系”的零假设了。这个例子的显着性水平为 0.05, 也就是说在推翻零假设这件事情上只有 5% 的概率是错的。
事实上,我们的统计结果还要更极端。标准误差(0.13)相比起回归系数(4.5)来说,是一个极小的数字,一个经验法则就是,当回归系数至少是标准误差的两倍或以上的时候,该系数极有可能具有统计学意义。使用统计软件还可以计算出这个例子中的假定值约为零,这就意味着如果整体人口的身高和体重真的不存在任何相关性的话,那么得到如此极端(或更加极端)结果的概率基本上为零。要记住,我们并没有证明身高略高的人的体重就一定更重,我们只不过表明了,由“变化的一生”样本得出的身高与体重相关性假如不为真的话,那会是一件极为反常的事。
通过基础的回归分析,我们还可以得出一个值得注意的统计值:用以衡量所有能够用回归方程表示的数据总和 R2。在“变化的一生”样本中,仅体重一项就有大量不同的数值,有一些人重于所有人的体重平均值,有一些人的体重还不足平均值,通过 R2, 我们便可以知道这些围绕在平均值周围的体重与身高两项因素之间的相关关系到底有多“亲密”,即回归系数。在这个例子中,答案是 0.25 或 25%。也就是说,我们的样本中有 75% 的体重数据无法在回归方程上表现出来。对于“变化的一生”项目的研究对象来说,影响他们体重的因素显然不仅身高这一项,别着急,有趣的内容马上就要讲到了。
但要记住的是,我们的基本原理并没有改变,无论是之前简单的身高与体重变量,还是现在的多个变量,只要将它们输入电脑上的统计软件,就会自动生成让残差平方和最小的回归系数与回归方程。
我们暂时还是以“变化的一生”为例,后面我将通过另外一个例子直观地告诉大家多变量回归分析是如何在我们的生活中创造奇迹的。首先,我们为“变化的一生”项目的研究对象的体重再增加一个解释变量:年龄。在电脑中输入相关的身高和年龄数据后,我们得到了如下的方程式:
体重 =-145+4.6×身高 +0.1×年龄 年龄的回归系数是 0.1,也就是说,在其他变量不变的条件下,年龄每增加一岁,体重相应地增加 0.1 磅。对于任意一组相同身高的人来说,年龄大的人的平均体重要高于年龄小的人,年长 10 岁表现在体重上就是体重重 1 磅。从方程式上看,虽然年龄对于体重来说并不是一个很显着的影响因素,但确实和我们在生活中看到的一致,该系数的显着性水平为 0.05。
你可能还注意到了身高的回归系数比之前增加了一点儿。当把年龄变量考虑进来后,我们对于身高对体重的影响有了一个更加精确的认识。样本里相同年龄的人中,也就是“当年龄为常量时”,身高每增加 1 英寸,体重增加 4.6 镑。
我们再加入一个变量:性别。这次就有一点不同了,因为性别只存在两种可能性:男性或女性。我们总不能把“男”和“女”放到回归方程式里吧?这时候我们需要用到二进制变量(又称虚拟变量)。在输入数据的时候,如果参与者是女性,我们就用 1 来表示;如果参与者是男性,我们就用 0 来表示。性别系数可以理解为,在其他因素不变的情况下对女性体重的影响。该系数为 -4.8,并没有出乎大多数人的意料,具体来说,就是对于相同身高和年龄的人来说,女性要比男性轻 4.8 磅。现在,我们可以开始领略多元回归分析的一些神奇之处了。我们知道女性一般要比男性矮一点儿,但好在我们已经将身高“控制”起来,因此最后呈现的系数也应该会表现出女性比男性矮的特点。最新的回归方程式如下:
体重=-118+4.3×身高+0.12×年龄-4.8×性别(女性为1,男性为0)
对于一位身高为65英寸的53岁女性来说,她的体重最有可能约为-118x4.3x65+0.12x53-4.8=163镑。对于一位身高75英寸的35岁男性来说,他的体重最有可能约为-118+4.3x75+0.12x35=209磅,我们之所以跳过回归方程式的最后一项(-4.8),是因为这个人不是女性。
当 R2 为 0 时,表示我们的回归方程式预测样本中个体体重的能力并没有比“平均值”好多少;当 R2 为 1 时,表示我们的回归方程式能够完美地预测样本中的每个人的体重)。
与职场歧视并无关系,例如更多女性倾向于选择半日制工作。那么,收入差距中有多少是因为工作量的不同,又有多少是因为职场歧视呢?我想这是所有人都愿意关心的问题。
回归分析可以帮助我们回答这个问题。但是,我们这次采用的方法就没那么直截了当了,会比之前解释体重的影响因素时略显复杂。我们会考虑其他一些影响收入的传统因素,如教育、工作经验、行业等,在控制这些因素相同的条件下,假如还存在显着的收入差距,那么就有可能是歧视因素在作祟。无法解释的收入差距的成分越多,职场歧视的嫌疑也就越大。举个例子,3 位经济学家对毕业于芝加哥大学布斯商学院约 2500 名工商管理硕士(MBA)的收入轨迹进行了跟踪研究,毕业时,男女毕业生的起薪大体相等:男性的收入为 13 万美元,女性的收入为 11.5 万美元。但是 10 年以后,他们的收入出现了巨大差异:女性的平均收入(24.3 万美元)比男性收入(44.2 万美元)低了 45%。在另一个大型样本中,1990~2006 年间毕业并进入职场的 18 万名 MBA 里,女性的收入要比男性低 29%。离开学校以后,我们的女同学都怎么了?
根据研究人员的调查,其实绝大部分收入差距与歧视因素的关系并不大。当有越来越多的解释变量加入分析中去,性别差异对收入的影响就变得越来越微不足道。例如,在校期间男性选择金融相关课程的人数比女性多,成绩平均分也高于女性,当将这些数据作为控制变量加入回归方程式之后,男女收入差距中无法解释的成分就下降到了 19%。再将毕业后的工作经历、不在公司的时间作为变量放入回归方程式去,男女收入差距中无法解释的成分又进一步降到了 9%。继续加入其他与工作特点有关的解释变量,如雇主类型和加班时长,男女收入差距中无法解释的成分已经不足 4% 了。
对于入行 10 年的雇员来说,他们之间存在的收入差距有 99% 都可以用非歧视性因素来解释,只有 1% 的概率与歧视有关。研究人员总结道:“我们发现有 3 个最主要的因素影响了男性和女性之间不断扩大的收入差距:MBA 学习期间不同的课程选择、事业中断的原因和时间长度的差别、每周工作长度的不同。这 3 个决定因素基本上可以解释男性和女性在完成 MBA 学业多年之后的收入差距。”
我希望通过我的介绍,大家能够认可多元回归分析的价值所在,尤其是在控制其他变量的条件下单独考虑某个解释变量给结果带来的影响。但是,我还没给大家举例说明这一神奇的统计学“万金油”到底是如何发挥作用的。在其他因素相同的情况下,当我们用回归分析法来考察教育和体重之间的关系时,假如“变化的一生”项目的研究对象在其他方面都不完全一样,那统计软件是如何控制身高、性别、年龄、收入等解释因素呢?
下面,我们就先分离出某个单一变量(比如教育)并观察其对体重的影响,为了让大家的头脑能够反应过来,我们先来设想如下情形。假设“变化的一生”项目的所有研究对象都被召集在同一个地方——马萨诸塞州的弗雷明汉,首先将他们按性别进行区分,然后再以身高为标准将男性和女性由高到矮作进一步划分,并安排到不同的房间里。现在,我们有一个房间里面全都是身高为 6 英尺的男性,隔壁房间是身高为 6 英尺 1 英寸的男性,以此类推,女性的情况也是如此。假如我们的研究对象数量足够多,那么还可以将每个房间里的人按收入状况再进行分类。最后,研究对象全都被安排进了面积不同的房间,每个房间里的人除了教育和体重以外其他方面全都相同,此时教育和体重是我们所关心的两个变量。有一个房间里全都是年龄为 45 岁、身高为 5 英尺 5 英寸、年收入在 3 万~4 万美元的男性,而隔壁房间里可能全是年龄为 45 岁、身高为 5 英尺 5 英寸、年收入在 3 万〜4 万美元之间的女性,诸如此类。
每个房间里个人的体重还是有所差别的,相同性别、身高和收入的人在体重上不一定都相同——但按理来讲,每个房间里的体重差异应该要小于整体样本的体重差异。那我们现在的目标就是,确定每个房间里剩余的体重差异里有多少成分可以用教育因素来解释,换句话说,教育和体重之间的最佳线性关系是什么?
现在就剩下最后一个挑战了,那就是如何解决这些房间内出现的不同的回归系数的问题。整个过程的重点就是,在保持其他因素不变的情况下,计算出一个单一的系数来对整个样本的教育和体重关系进行一个最佳描述。我们想要看到的是,用这个唯一的系数使所有房间内不同体重值的残差平方和为最小。那怎样的一个系数才能达到如此效果呢?答案就是回归系数,因为在性别、身高和收入相同的条件下,回归系数能够最好地描述教育和体重之间的线性关系。
一项对包含 10308 名英国公务员的样本的跟踪研究就试图理清这其中的差别。这一次雇员们还是按照行政级别进行划分——高级、中级和低级,只不过这一次参与者还必须完成一份 15 个题目的问卷,这份问卷主要是评价他们的“决策力或控制力”水平,其中设置的问题包括“你可以选择自己在工作中从事哪些项目吗?”对应的选项按程度划分(“从不”到“经常”),还有陈述句,比如“我在工作中可以决定何时停下来休息”。研究者们发现整个观察过程中“控制力低”的雇员患上冠心病的风险要高于“控制力高”的雇员。同时,研究人员还发现对工作要求高的雇员患心脏疾病的风险并没有比其他人高,在社会认可度低的岗位上工作的雇员也没有表现出容易患上心脏病的倾向。因此,似乎只有对工作缺乏控制力和话语权才是“生命杀手”。
1981~1993 年间,已发表 36 项研究成果关于此类课题,其中绝大多数的研究成果都发现工作疲劳和心脏病之间存在显着的正相关关系。
其次,研究人员探索并发现了相关的生物学证据,解释为什么这一特殊的工作压力能够导致健康状况的恶化。要求严格但控制力低的工作环境能够导致一系列生理反应(如释放与压力有关的荷尔蒙),长此以往会增加患心脏类疾病的风险,甚至连动物研究都为解释其病变原理发挥了作用。研究人员发现,地位低的猴子和拂狒(它们与权力系统中处于底层的公务员的境遇有着相似之处)与地位高的同类在某些生理指标上存在差异 , 使得前者更容易患上心脏血管疾病。
以下就是让回归分析这一非凡的工具沦为“邪恶”工具的 7 个最常见的错误。
用回归方程式来分析非线性关系。
(解释变量)和每场 18 洞练习的平均杆数(因变量)之间的关系,如你所见,两者之间并不存在一致的线性关系。
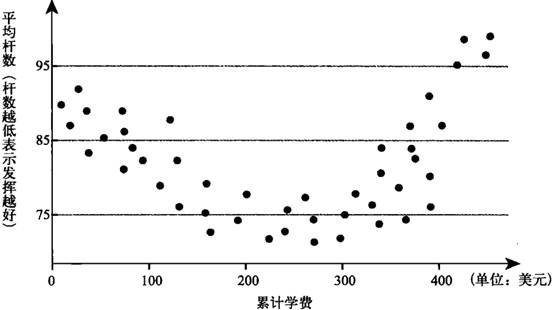
上图中并非完全没有规律,只不过是难以用一条直线来描述罢了。前几节高尔夫球课使我的杆数快速降了下来,因此在这个阶段,我的课程数与杆数是呈负相关关系的,斜度为负,也就是说,上课降低了我的杆数(对于高尔夫球来说这是一件好事)。
但是,当我的学费累计交到了 200〜300 美元时,这个阶段的课程似乎对我的球场表现没有太大的帮助。高尔夫球课程与我的成绩之间似乎不存在一个明确的关系,因此斜度为零。
随着上课的次数越来越多,我的成绩甚至出现了下滑。当累计学费达到 300 美元以上,增加的课程反而使我的杆数越来越高,在这个阶段斜率就为正了(后面的内容我会为大家解释为什么是发挥不佳导致了学习更多的课程,而不是学习更多的课程导致了发挥不佳)。
相关关系并不等同于因果关系。如我之前所说,回归分析只能证明两个变量之间存在关系,至于是不是其中一个变量发生变化就一定能导致另一个变量也发生变化,仅凭数据我们无法给出证明。事实上,一个并不十分严谨的回归分析也能在两个完全不相关的变量之间找到显着且有统计学意义的关系。假设我们正在探寻过去 20 年里美国的自闭症病例不断增多的原因。我们的因变量——也就是我们正在试图对其做出解释的现象——需要对自闭症进行量化,比如每千名某个年龄段儿童中自闭症的病例数量。与此同时,假如我们将中国的人均年收入看作一个解释变量,我们肯定能够在过去 20 年里激增的中国人均收入和上升的美国儿童自闭症确诊率之间发现一个正相关且具有显着统计学意义的关系。
这是为什么呢?因为它们在同一时期都出现了快速上涨的趋势。但是,我高度怀疑即使中国出现经济衰退,美国的自闭症儿童也不会因此减少。
因果倒置。假如 A 与 B 之间存在统计学关系,我们不能直接推出 A 导致 B,因为完全有可能是 B 导致 A。还记得刚刚的那个高尔夫球课的例子吗?我当时已经暗示了这种现象的存在。在我搭建的解释模型里,击球成绩始终是因变量,解释变量一直锁定在累计课程上。也就是说,上的课越多,成绩越差!一种解释是我的高尔夫球教练教得很差,但另一种更加说得通的解释是,我在状态不好时总是会想着多上几节课——状态不佳导致了更多的课程,而不是相反的情况。(对于这类问题来说,我们在方法论上有多种解决办法。例如,我可以将这个月的高尔夫球课作为下个月成绩的解释变量)。
因果关系有时候是双向的。假设你手头正在做的一项调查显示,美国在 K-12(指从幼儿园到 12 年级儿童教育)上投入多的州的经济增长率要高于 K-12 项目投入少的州。但就算这两个变量之间的正相关关系再显着,我们也无法从中看出因果关系的方向。我们既可以说 K-12 教育的投入推动了经济增长,也可以认为只有那些经济实力雄厚的州才有钱在 K-12 教育上投入更多,因此是增长的经济带来了教育的投入。还可以说,教育支出推动了经济增长,继而为进一步加大教育投入提供了可能,即它们互为因果。
关键在于,我们不应该使用那些(我们正在花大力气解释的)受结果影响的解释变量,不然的话,因和果将会永无休止地纠缠下去。举例来说,解释 GDP 增长时,在回归方程中加入失业率因素是不合适的,因为失业率很显然会受 GDP 增长率的影响。或者换一个角度来看,通过回归分析,发现失业率的下降会促进 GDP 的增长,这样的结论是可笑的、没有任何意义的,因为为了降低失业率,通常的做法是促进 GDP 的增长。
变量遗漏偏差。下次当你在报纸上读到类似于《常打高尔夫易患心脏病、癌症和关节炎》这类标题时,千万不要轻信。高尔夫球球员患上这些疾病的概率比不打高尔夫球的人高——关于这一点我一点儿都不觉得奇怪,但我同时也认为打高尔夫球有益健康,因为它不仅能够丰富你的社交生活,还能为你提供适当的运动量。我应该如何在这两个截然不同的观点之间进行取舍呢?非常容易。无论什么研究,在量化高尔夫球对健康的影响时都必须正确控制“年龄”变量,通常来说,年龄越大,打高尔夫球的时间和机会越多,尤其是在退休之后。在打高尔夫球这个课题上,任何没有将年龄作为解释变量的研究都不可避免地遗漏了一个事实,那就是打高尔夫球的人总体上比不打高尔夫球的人年长。因此,杀人的不是高尔夫球,而是衰老,而且那些正在老去的人恰巧对打高尔夫球乐此不疲。如果将年龄纳入回归分析中去,得到的结论将很有可能是另外一幅光景:在年纪相仿的一群人中,打高尔夫球可能还会对严重疾病的预防起到正面的效果。这跟前面提到的报纸标题有着天壤之别。
在这个例子中,年龄是一个被遗漏的重要变量。当我们用回归方程式解释打高尔夫球与心脏病或其他疾病的关系时,如果将年龄因素排除在外,那“打高尔夫球”就会超出自身的解释作用,而相当于扮演了两个解释因素的角色:它不仅告诉我们打高尔夫球对心脏病的影响,而且还告诉我们年纪的增长对心脏病的影响(因为打高尔夫球的人通常比其他人要年老一些)。用统计学术语来表达,就是打高尔夫球这个变量“覆盖”了年龄这个变量的影响。也就是说,这两种不同的影响在分析中被混为一谈,
高度相关的解释变量(多元共线性)。在一个回归方程式中,假如两个或两个以上解释变量彼此之间高度相关,那么回归分析的结果将有可能无法分清每一个变量与因变量之间的真实关系。举例说明,假设我们想要知道吸毒对 SAT 考试分数的影响,我们会询问研究对象是否吸食过可卡因或海洛因
让分析变得模糊。丈夫和妻子的受教育程度存在着相当大的相关性,以至于我们无法通过回归分析得出一个有意义的关于某个家长的教育程度系数(就好像我们难以区分可卡因和海洛因对考试的影响一样)。
脱离数据进行推断。
出结论时就明确地规定了适用范围,可以说具体得不能再具体了:“从事缺乏控制力的工作将会增加未来患上冠心病的风险,该结论仅适用于受雇于政府部门的男性和女性。”
变量过多。
假如变量过多,尤其当无关变量过多的时候,回归分析的结果就会被冲淡或稀释。
有大量发表的专家研究最后被证明是错误的。希腊医生和流行病学家约翰·艾奥尼蒂斯对 3 本最有声望的医学期刊里刊登的 49 篇学术研究论文进行了统计,每一篇论文的研究发现都被转引了至少 1000 次,但其中差不多有 1/3 的研究成果都被后续的研究否定了。(例如,有一些研究是支持雌激素补充疗法的)。根据艾奥尼蒂斯博士的观察,在已经出版的科学论文中,差不多有 1/2 最终会被证明是错误的。他的研究成果刊登在《美国医学协会学报》上,有趣的是这就是他所研究的 3 本期刊中的其中一本。这难免令人产生困惑:假如艾奥尼蒂斯博士的研究发现是正确的,那他的研究发现就很有可能是错误的。
本章精选的所有警示其实都可以浓缩为两个基本经验。第一,设计一个好的回归方程式,想清楚应该考虑哪些变量、应该从哪里收集数据,一个好的方程式要比统计计算本身更加重要。这个过程可以通过对方程式的评价和回归方程的具体化来实现。
第二,与绝大部分统计推断一样,回归分析始终以观察样本为立足点。两个变量之间的相关关系就像是犯罪现场的一个指纹,能够为我们指出正确的方向,但在大多数时候还不足以定罪(有些时候在犯罪现场发现的指纹甚至都不是凶手的)。对于任何回归分析来说,都需要在以下方面得到理论支持:为什么方程式里要有这些解释变量?通过其他学科领域是否也能解释这个分析结果?例如,我们为什么会认为穿紫色鞋子可以提高 SAT 考试数学部分的成绩?为什么吃爆米花可以帮助预防前列腺癌?分析得出的结论需要具有可复制性,至少也得与其他科学发现相一致。
下面就来介绍一些隔离“治疗”效果最常用的方法。
随机控制实验。
样本数量越大,随机分配的作用就越明显,实验组和对照组的相似性也越强。
医学试验就是典型的随机控制实验。理想的情况是“双盲”的临床试验,这意味着无论是病人还是医生都不知道哪一组是治疗组,哪一组是对照组。但如果治疗里包含了手术(心脏外科医生当然知道要给哪些病人做搭桥手术),那“双盲”显然是不可能了。但即使要做手术,病人依然可以被蒙在鼓里,因为就算进了手术室,他们也不知道自己是否接受了心脏搭桥。我最欣赏的研究之一是一份有关某种缓解膝盖疼痛的手术评估报告,治疗组的病人接受了膝盖手术,而对照组病人则接受了一次“冒充手术”,医生只在这组病人的膝盖部位划了 3 道极小的口子,“假装在给他们动手术”。最后的结果是,真正的手术在缓解膝盖疼痛方面并没有比“冒充手术”有效。
《纽约时报》报道:“无论是哪个国家的研究人员,一个他们达成共识的与长寿相关的社会因素就是教育。一个人受教育程度的高低与寿命长短的相关性比种族和收入因素都要显着。”但至少到目前为止,这还只是一个相关关系。在其他情况都相同的前提下,更多的教育是否就能够带来更健康的身体?如果你把教育看作一种“治疗”,那么接受更多的“治疗(教育)”是否就能保证你活得更久?
这是一个看似不可能得到回答的问题,因为选择接受教育的人与不希望读更多书的人肯定在某些方面是不一样的。高中学历与本科学历的人之间的差别绝不仅限于大学 4 年的教育,在那些选择继续求学的人当中,极有可能存在某些他们所共有的除了教育以外的隐藏特性,从而使得这些人更加长寿。假如这是真的,那么让那些原本没想过继续念书的人上大学;对延长他们的寿命并不会有帮助。健康状况的改善不能归功于提高的教育程度,而是来自于那类选择提高自身教育程度的人所共有的特质。
非对等对照实验。有些时候研究治疗效果最佳且可行的方式,并非完全随机地分配实验组和对照组。当环境不允许我们进行随机分配的时候,我们当然希望最终的实验组和对照组能够大体相似,不对结论的准确性产生影响。好消息是,我们有一个实验组,一个对照组。坏消息是,任何非随机分配都会产生偏见,至少是有存在偏见的可能性。就算你认为你的分组毫无破绽,但或许在实验组和对照组之间还有一些难以察觉的差异,正是这些差异影响了小组成员的分配和组成,从而产生跟现实有偏差的结论,这就是我们所说的“非对等对照”。
一个非对等对照组依然可以成为非常有用的工具。让我们回过头来思考一下本章开头提出的那个问题:进入一所顶尖大学学习真的会给人的一生带来巨大的优势吗?
我们所不知道的是,接受像哈佛或耶鲁大学这类顶尖大学的精英教育会产生怎样的效果?从这些名牌大学毕业出来的人之所以能够成功,到底是因为他们当初在跨入校门时就已经才华出众,还是因为这些大学通过精选优秀人才、培养他们的竞争力而使得他们的“附加值”增加,又或者两者都有?
我们还是不能通过随机实验的方法来回答这个问题。很少有高中毕业生愿意被随机分配到一所大学就读,哈佛和达特茅斯大学肯定也不愿意接收随机分配给它们的学生。研究似乎陷入了僵局,到底怎么样才能检验大学教育的效果呢?开动脑筋就能找到出路!两位经济学家斯塔西·戴尔和阿兰·克鲁格发现,其实有很多学生在高中毕业时会同时申请多所大学,通过对这一事实的“挖掘”,研究出现了转机。一些学生被名牌大学录取之后便高高兴兴地去报到了,而有一些学生在收到名牌大学的录取通知书后,经过再三考虑,还是去了普通大学或学院深造。于是现在我们就有了一个实验组(进入名牌大学学习的同学)和一个非对等对照组(凭才华和实力足以进入名牌大学却选择去竞争没那么激烈的高校学习)。
戴尔和克鲁格对两个组学生的纵向数据进行了分析。虽然这不是一个苹果对苹果的完美比较,而且收入只不过是人生成就的一部分,但他们的发现应该能够舒缓高中生及其父母的紧张情绪。毕业于名牌大学的人在收入方面并没有超过实力相当,但选择就读一般大学的人,唯一的例外就是出生于低收入家庭的人,他们从名牌院校毕业后的收入会有明显的增长优势。戴尔和克鲁格的方法有效地将实验效果(在名牌大学读 4 年书)从选择效果(最有才华的学生都被名牌大学挑走了)中剥离了出来。阿兰·克鲁格在《纽约时报》上撰文指出,“相比起毕业证书上的学校名字,正确认识自己的兴趣、抱负和能力更能成就人的一生”,这其实也间接回答了本章开头所提出的那个问题。
差分类差分实验。
假如美国政府推出了减税政策,经济就会跟着好转,
的确,政府的减税政策或许正好在某个时间点出台,但在同一时期可能还有其他“介人”因素在发挥作用:越来越多的女性进入大学学习,互联网以及其他科技创新正在提升美国工人的生产效率,
任何“前与后”类的分析均面临着一个挑战,那就是仅凭一件事情紧随另一件事情的发生,并不能推断两件事情之间存在因果关系。
“差分类差分”法可以通过两个步骤来明确某个介入因素的效果。首先,我们对某个群体接受某项介入因素或治疗之前和之后的数据进行比较,例如推广促进就业政策之前和之后某个县的失业率变化情况。其次,我们将这些数据与另一个没有推出就业政策的同类县同期的失业率情况进行比较。
重要的是,用于分析的两个对象除了是否有介入因素,其他方面的情况基本上都相似;因此,两个对象的观察结果若存在任何显着差异,就应该被认为是所评估的项目或政策的效果。举个例子,假设伊利诺伊州的一个县为了应对高失业率 , 推出了一个就业培训项目,但在接下来的两年时间里,失业率依然呈上升走势,这是不是就意味着就业培训项目失败了?谁能告诉我们答案?
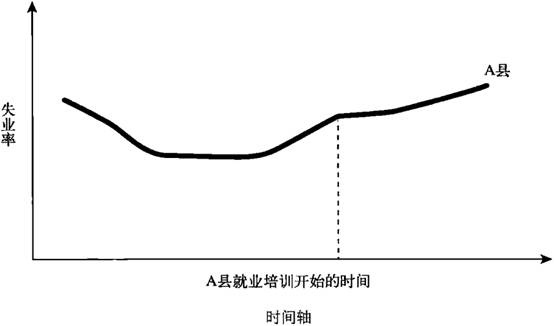
也有可能存在其他宏观经济因素的作用,如经济的持续不景气等。在“差分类差分”法的指导下,我们对同期两个县的失业率变化情况进行比较,其中一个县推广了就业培训项目,另外一个县并没有推广,除此之外两个县在其他方面都必须保持一致:相同的工业构成、相似的人口结构等。那么,推广了就业培训项目的县在失业率数据上的变化相比起另一个没有推广该项目的县,呈现了一幅什么光景呢?通过比较两个县相同时间段内的失业率变化,我们就能理性地推断出就业培训项目的效果了。这就是“差分类差分”,前一个差分表示项目推广前后的失业率变化,后一个差分指的是两个县同期的失业率变化差异。另一个没有推广就业培训项目的县在研究过程中扮演的是对照组的角色,有利于我们更好地理解项目实施前后的数据变化,因为对照组会受到跟实验组一样的宏观经济的作用。最初我们认为就业培训项目一无是处(因为在项目实施之后失业率变得更高了),但是对照组为我们展示了更加糟糕的就业情况,因此通过综合比较和分析,就业培训项目的正面作用就显现出来了。
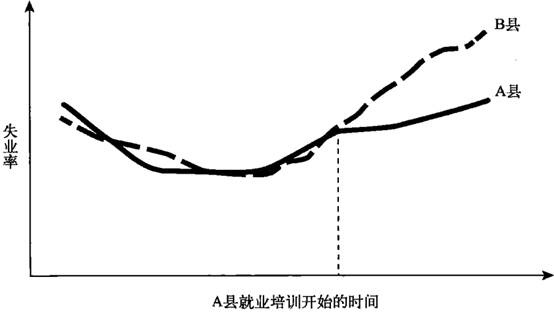
不连续分析实验。实验组和对照组还存在一种设置方式,就是将那些刚好符合介入或治疗条件的对象,以及以毫厘之差错失治疗机会的对象进行比较。那些刚好超过或略微不足规定条件(如考试分数或最低家庭收入等)的个人,其实在许多重要方面与实验组里的个人相差无几,而一组对象接受治疗、另一组对象不接受治疗的人为划分其实本身就是非常任意的。因此,比较这两类对象可以为我们提供有关介入或治疗效果的有益参考。
假设某个学区要求各个学校利用暑假的时间为成绩不理想的学生开设补习班,主管教育的领导想要知道暑期补习班项目是否具有长期推广的价值。当然,如果只是简单地比较参加补习班的学生和不参加补习班的学生,结果将会是毫无意义的。那些学生之所以会出现在暑期补习班里就是因为他们的成绩不好,就算暑期补习班的效果立竿见影,这些学生还是难以在考试中超过班上其他不需要参加补习班的同学。我们真正关心的是,这些学生在参加完补习班之后的成绩与参加补习班之前相比是不是提高了。是的,我们可以组织一些控制对照实验来将成绩不理想的学生随机分配到暑期补习班组或“闲置在家”组,但这可能会剥夺一些想要寻求上进的学生提高成绩的机会。
所以,我们的实验组和对照组应该来自那些正好在班上成绩居中的同学,有一些学生刚好被老师安排到补习班,有一些学生差一点儿就失去了自由自在的暑假时光。设想一下:那些在期中考试中成绩不及格的学生肯定与考试及格的学生是不一样的,但一个分数为 59 分(不及格)的同学与一个分数刚好为 60 分(通过考试)的同学呢?如果那些在期中考试中成绩不及格的学生必须参加补习班,那么一个合理且有意义的实验组和对照组就应该在那些差一点儿就及格的学生(参加补习班)和差一点儿就不及格的学生(不需要参加补习班)中产生,这两组学生的期末成绩将会是我们关注的重点。
因果关系是一根难啃的骨头,我们有时候甚至连明显得不能再明显的原因和结果都无法确定。为了了解某种介入手段或治疗真正的效果,我们需要看到“反现实——事实的背面”,即假如没有介入手段或治疗会发生什么。但是在许多时候,“事实的背面”却没有那么容易甚至不可能被发现。
结束语
1930 年美国总统赫伯特·胡佛宣布大萧条结束,但其所参考的依据尽是些不准确的过时数据。他在国情咨文中告诉全体国民美国有 250 万人没有工作,但实际的失业人数已经高达 500 万人,而且还在以每周 10 万人的速度增加。
有越来越多的证据表明,橄榄球运动过程中产生的脑震荡和其他大脑损伤能够导致严重且永久的神经伤害。(拳击手和曲棍球运动员身上也存在类似的现象。)许多知名的职业橄榄球运动员都曾在公众面前分享过他们退役后与抑郁、记忆丧失以及痴呆等疾病抗争的故事。最令人感到心酸的莫过于前芝加哥熊队安全队员、“超级碗”冠军戴夫·杜尔森,他开枪结束了自己的生命,在遗书中他明确指示家人将他的大脑捐献给相关机构用于科研。
在一次随机电话调查中,有 1000 名联盟生涯在 3 年或 3 年以上的前职业橄榄球运动员接受了采访,年龄在 50 岁以上的运动员中有 6.1% 被诊断患有“痴呆、阿尔茨海默症或其他记忆力相关疾病”,是相同年龄段美国平均水平的 5 倍。在年轻运动员群体中,类似疾病的诊断率达到了美国平均水平的 19 倍。至今已有数百名前美国职业橄榄球联盟运动员将联盟和运动头盔制造商告上了法庭,理由是他们涉嫌故意隐瞒有关头部损伤危害的信息。
北卡罗来纳州州立大学运动脑震荡研究中心的凯文·加士奇维茨在北卡罗来纳州橄榄球队的每一位队员头盔内嵌入了一个感应器,以便记录下运动过程中队员受到的头部撞击的力度和性质。根据他所获得的数据,运动员日常每受到一次头部撞击,就相当于坐在一辆时速为 25 迈的车里突然遇到车祸时脑袋撞上挡风玻璃所受到的撞击。
但在这个例子中,有一些信息是我们无法知晓的。到目前为止,我们已经发现的有关大脑损伤的证据是否就能全权代表所有职业橄榄球运动员退役后所面临的神经病变风险?还是说,遭遇不幸的人只是所有运动员中的“一小撮”,即统计学上的“异常值”?就算真的是所有橄榄球运动员在晚年患上神经紊乱的风险高于常人,我们也无法证明两者之间的因果关系:可能是爱好并从事橄榄球(或拳击、曲棍球)运动的人天生就容易患上此类疾病;也有可能是其他一些因素,如注射类固醇导致了他们晚年的神经疾病。
假如不断有证据表明,橄榄球运动与永久性大脑损伤之间存在清晰的因果关系,那么一个严峻且现实的问题就摆在了运动员(以及青少年运动员的家长)、教练员、律师、NFL 官员,甚至政府有关人员的面前
哪位教授的教学效率最高?
答案是:经验偏少又在非名牌大学取得学士学位的那些教授们。他们的学生在初级课程的标准考试中的成绩普遍较好,而且他们在教学评估中得到的学生评价也通常较好。显而易见,这些年轻、充满干劲的老师对待教学比脾气暴躁的哈佛大学博士老教授要认真负责得多。那些老人家至今还在用 1978 年的陈旧教案来教学生,他们或许还以为演示文稿软件(PPT)是某种功能饮料——除非他们连什么是功能饮料都没见过。根据数据,我们早就应该将这些年龄过大的教授解雇了,或者让他们有尊严地退休。
不过,我们先别急着解雇可人。空军学院的研究还有另一个发现——学生的长远表现。卡瑞尔和韦斯特发现,在数学、科学等学科的初级课堂上,经验更丰富、资格更老的老师教出来的学生在接下来的中级、高级课程中的表现要优于年轻教师教出来的学生。一个符合逻辑的推理就是那些资历尚浅的老师更倾向于在初级课堂上“教学生如何去应付考试”因此他们的学生在考试中的分数通常比较高,学生自然会感到开心,给老师的评价自然也不会差。
但是,那些上了年纪的、脾气固执的资深教授们(我们在前一段的内容中差点儿就解雇了他们)更关注的是教授重要的理论和概念,而不是考试,这对于学生的进一步学习以及一生都会是受益匪浅的。
在管理家庭财产的问题上,谁能作决定——男人还是女人?在发达国家,夫妻两人可就这个问题在他们的婚姻顾问面前吵上一整天;但在贫困国家,这个问题决定了家里的小孩能否吃饱饭。从古至今,人们一直存在一个观念,那就是家中的女性总是将孩子的健康和幸福置于一个极高的位置,而家中的男性更倾向于把工资都花在喝酒或其他消遣上。往差了说,这种观念只会让一成不变的偏见更加根深蒂固;往好了说,我们只能认为这是一个难以证明的观点,因为一个家庭的财政在一定程度上受到很多因素的影响。丈夫和妻子对家中的共同财产都有支配权,那么我如何将二者的消费选择进行控制并逐个分析呢?
面对这个如此复杂和微妙的问题,迪弗洛没有选择逃避。她甚至还为此进行了一个令人无比着迷的自然实验。在科特迪瓦,家中的男性和女性共同承担种植庄稼的工作,而且一个长久以来约定俗成的做法是,男性和女性各自耕种不同的经济作物,男性种可可、咖啡等,女性种芭蕉、椰子等。从研究者的角度,这种天然安排的好处是男女种植的不同经济作物对雨量的需求恰好相反:在可可和咖啡丰收的年份里,家中的男性会拥有更多的可支配收入;在芭蕉和椰子丰收的年份里,家中的女性会拥有更多的可支配收入。
现在,我们只需要将刚才那个棘手的问题提出来:在科特迪瓦的这些家庭中,孩子们是希望爸爸的作物丰收从而让生活变得更好,还是希望妈妈的作物丰收从而让自己过得更幸福?
回答是:当女性的收入提升时,她们会将手中余钱的一部分用于改善家庭的伙食,但男性通常不会这么做。
3〜6 个月的准妈妈,想办法让她们更经常地来逛商场。《纽约时报》的一位签约作家全程跟随了塔吉特的一个预测分析团队来了解他们是如何定位并吸引孕妇的。
第一步非常简单。塔吉特向会员提供了迎婴礼物登记服务,怀孕的会员可以在孩子出生前登记领取婴儿礼品。这些女性已经是塔吉特的购物者,而且她们会主动告诉商场自己怀孕的消息。此外统计专家还发现,其他那些与上述消费者有着相似消费倾向的女性可能也怀孕了。举个例子,怀孕的女性通常会将沐浴露换成无香味的,她们会开始购买维生素类保健品,购买棉球等卫生用品时会选择大包装的。塔吉特公司的预测分析专家们精挑细选出 25 种商品,这些商品共同构成了一个“怀孕预测得分”体系,所有分析的最终目标就是向怀孕女性发放相关商品的优惠券以吸弓丨她们前来购买,并最终让她们成为塔吉特公司的长期消费者。
但事实上,商家已经知道你既不打保龄球也不修剪草坪,这些广告只不过是一个幌子,为了掩盖他们知道你怀孕的事实。